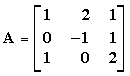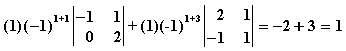4.3:Ορίζουσες

Σε κάθε τετραγωνικό πίνακα Α αντιστοιχούμε έναν αριθμό |Α| τον οποίο ονομάζουμε ορίζουσα του Α. Για τον ορισμό της ορίζουσας του Α, χρειαζόμαστε την έννοια της μετάθεσης των στοιχείων ενός σύνολου.
Έστω σύνολο Κ = { α₁ , α₂ , . . . , α_ν }. Μετάθεση των ν στοιχείων του Κ ονομάζεται κάθε διατεταγμένη ν-άδα στην οποία κάθε στοιχείο του Κ εμφανίζεται ακριβώς μια φορά. π.χ. εάν Κ = { 1, 2 , 3 }
Οι διατεταγμένες 3-άδες
(1,2,3) , (1,3,2) , (2,1,3) , (2,3,1) , (3,1,2) , (3,2,1) αποτελούν όλες τις πιθανές μεταθέσεις των 3 στοιχείων του Κ.
( Αυτές είναι 3! = 3 2 1 = 6 τον αριθμό ).
Γενικά μπορεί να αποδειχθεί ότι κάθε σύνολο με ν στοιχεία έχει ν! μεταθέσεις.
Θα λέμε ότι μια μετάθεση του συνόλου Κ = { 1,2, . . . , ν } παρουσιάζει αντιστροφή εάν κάποιο στοιχείο προηγείται στην σ κάποιου μικρότερού του.
π.χ. εάν Κ = { 1,2,3 },
στην μετάθεση (3,2,1) παρατηρούνται 3 αντιστροφές.
Mια μετάθεση του συνόλου Κ ονομάζεται περιττή (άρτια) εάν σ' αυτή παρατηρείται περιττός (άρτιος) αριθμός αντιστροφών.
Το πρόσημο μιας μετάθεσης σ του Κ, συμβολίζεται με sgn(σ) και ορίζεται ως εξής:

sgn(σ) {

+1 εάν η σ είναι άρτια -1 εάν η σ είναι περιττή

Μετά από την αναφορά που κάναμε στην έννοια των μεταθέσεων μπορούμε να ορίσουμε την ορίζουσα.
Ορισμός : Έστω τετραγωνικός πίνακας Α = [α_ij] μεγέθους νxν. Ονομάζουμε ορίζουσα του πίνακα Α τον αριθμό sgn(σ)α_1σ1α_2σ2 . . . α_νσν όπου το άθροισμα θεωρείται πάνω σε όλες τις μεταθέσεις σ = ( σ₁,σ₂ , . . . ,σ_ν ) του συνόλου Κ= {1,2, . . . ,ν }.
Παράδειγμα : Έστω Σύμφωνα με τον ορισμό που δώσαμε |Α| = sgn(σ)α_1σ1α_2σ2 όπου το άθροισμα θεωρείται πάνω σ'όλες τις μεταθέσεις σ = ( σ₁,σ₂) του Κ = {1,2}. Το Κ έχει δύο μεταθέσεις τις (1,2) και (2,1). Η πρώτη είναι άρτια ενώ η δεύτερη περιττή. Άρα |Α| = (+1)α₁₁α₂₂+(-1)α₁₂α₂₁ Άσκηση : Να προσδιορισθεί η ορίζουσα του χρησιμοποιώντας τον ορισμό που δώσαμε προηγουμένως. Απάντηση

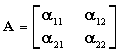
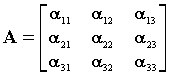
Θεώρημα 4.4

Η ορίζουσα ενός πίνακα Α και του αναστρόφου του ΑΤ είναι ίσες. Δηλαδή |Α| = |ΑΤ|

Παρατήρηση Από το Θεώρημα 4.4 προκύπτει το εξής: Εάν έχουμε ένα θεώρημα , το οποίο είναι σχετικό με ορίζουσες και το οποίο αναφέρεται στις γραμμές ενός πίνακα, το ίδιο ισχύει και για τις στήλες του (και αντίστροφα).
Τα επόμενα θεωρήματα αναφέρονται επίσης σε ιδιότητες της ορίζουσας.

Θεώρημα 4.5

Εάν ο Α έχει μια γραμμή (στήλη) μηδενική, τότε |Α| = 0.

Άσκηση : Να αποδειχθεί το Θεώρημα 4.5 . Απάντηση

Θεώρημα 4.6

Εάν εναλλάξουμε δύο γραμμές (στήλες) ενός πίνακα τότε η ορίζουσα αλλάζει πρόσημο.

Θεώρημα 4.7

Εάν ο Α έχει δύο γραμμές (στήλες) ίδιες, τότε |Α| = 0.

Άσκηση : Να αποδειχθεί το Θεώρημα 4.7 χρησιμοποιώντας το Θεώρημα 4.6 Απάντηση

Θεώρημα 4.8

Εάν Α = [αij] τριγωνικός πίνακας μεγέθους νxν, |Α| = α11α22 . . . ανν.

Απόδειξη

Θεώρημα 4.9

(i) Εάν πολλαπλασιάσουμε μια γραμμή (στήλη) ενός πίνακα με αριθμό, τότε η ορίζουσα πολλαπλασιάζεται με τον ίδιο αριθμό. (ii) Αν προσθέσουμε ένα πολλαπλάσιο μιας γραμμής (στήλης) σε μια άλλη γραμμή (στήλη) τότε η ορίζουσα παραμένει η ίδια.

Εάν από ένα τεραγωνικό πίνακα Α = [α_ij] μεγέθους νxν αφαιρέσουμε την i-γραμμή του και την j-στήλη του, τότε μένει ένας τετραγωνικός πίνακας Μ_ij μεγέθους (ν-1)x(ν-1). Ελάσσων ορίζουσα του στοιχείου α_ij του πίνακα Α ονομάζουμε την ορίζουσα του πίνακα Μ_ij .
Ο συμπαράγοντας του στοιχείου α_ij συμβολίζεται με Α_ij και ορίζεται ως εξής Α_ij : (-1)^i+j |M_ij| .
Παράδειγμα : Εάν έχουμε
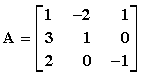
Eάν σε προηγούμενη άσκηση είδαμε ότι |Α| = α₁₁α₂₁α₃₃ + α₁₂α₂₃α₃₁ + α₁₃α₂₁α₃₂ - α₁₁α₂₃α₃₂ - α₁₂α₂₁α₃₃ - α₁₃α₂₂α₃₁
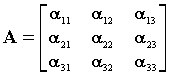
Το άθροισμα των γινομένων που μας δίνει την ορίζουσα του Α, μπορεί επίσης να γραφεί με τους εξής τρόπους:
|A| = α₁₁(α₂₂α₃₃ - α₂₃α₃₂) + α₁₂(α₂₃α₃₁ - α₂₁α₃₃) + α₁₃(α₂₁α₃₂ - α₂₂α₃₁)     = α₂₁(α₁₃α₁₂ - α₁₂α₁₃) + α₂₂(α₁₁α₃₃ - α₁₃α₃₁) + α₂₃(α₁₂α₃₁ - α₁₁α₃₂)     = α₃₁(α₁₂α₂₃ - α₁₃α₂₂) + α₃₂(α₁₃α₂₁ - α₁₁α₂₃) + α₃₃(α₁₁α₂₂ - α₁₂α₂₁) Δηλαδή |Α| = α₁₁Α₁₁ + α₁₂Α₁₂ + α₁₃Α₁₃     = α₂₁Α₂₁ + α₂₂Α₂₂ + α₂₃Α₂₃     = α₃₁Α₃₁ + α₃₂Α₃₂ + α₃₃Α₃₃
Mε άλλα λόγια παρατηρούμε ότι η ορίζουσα του Α ισούται με το άθροισμα των γινoμένων των στοιχείων μιας οποιαδήποτε γραμμής του με τους αντίστοιχους συμπαράγοντες. Αυτό δεν ισχύει μόνον για πίνακες μεγέθους 3x3, αλλά γενικά για κάθε τετραγωνικό πίνακα. Συγκεκριμένα έχουμε το εξής θεώρημα.

Θεώρημα 4.10:

Έστω τετραγωνικός πίνακας Α = [αij] μεγέθους νxν. Τότε |Α| = αi1Αi1 + αi2Αi2 + . . . + αiνΑiν για οποιαδήποτε γραμμή i του Α ( |Α| = α1jΑ1j + α2jΑ2j + . . . + ανjΑνj για οποιαδήποτε στήλη j του Α )

Παράδειγμα    Εάν
|A| = (1)A₁₁ + (0)A₂₁ + (1)A₃₁

---