4.4:Συστήματα εξισώσεων

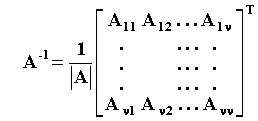
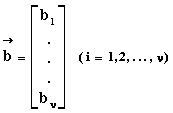Σ' αυτό το υποκεφάλαιο θα εξετάσουμε κυρίως την σχέση που υπάρχει μεταξύ των λύσεων ενός γραμμικού συστήματος ν εξισώσεων με ν αγνώστους, με τις έννοιες του αντίστροφου πίνακα και της ορίζουσας.

Θεώρημα 4.11

Για κάθε τετραγωνικό πίνακα Α = [αij] μεγέθους νxν, οι παρακάτω προτάσεις είναι ισοδύναμες : (1) Ο Α είναι αντιστρέψιμος (2) Tο σύστημα Α = έχει μια και μοναδική λύση για κάθε ν (3) Tο ομογενές σύστημα Α = έχει για μόνη λύση του, την μηδενική. (4) |A| 0 (5) Ο βαθμός του πίνακα Α (ο οποίος συμβολίζεται με ρ(Α) ) ισούται με ν.

Άσκηση
a) Nα αποδειχθεί ότι οι προτάσεις (4) και (5) είναι ισοδύναμες
b) Nα αποδειχθεί ότι οι προτάσεις (3) και (5) είναι ισοδύναμες
Αποδείξεις

Το Θεώρημα 4.11 μας δίνει ικανές και αναγκαίες συνθήκες για να είναι ένας πίνακας Α αντιστρέψιμος. Το επόμενο θεώρημα μας λέει πως θα βρίσκουμε τον αντίστροφο του Α.

Θεώρημα 4.12

Έστω τετραγωνικός πίνακας Α = [αij] μεγέθους νxν. Εάν |Α| 0 ο Α είναι αντιστρέψιμος και

Δηλαδή για να βρούμε τον αντίστροφο του Α, αρκεί να πολλαπλασιάσουμε τον ανάστροφο του πίνακα των συμπαραγόντων των στοιχείων του, με τον αριθμό .
Ο ανάστροφος του πίνακα των συμπαραγόντων των στοιχείων του Α, συνήθως συμβολίζεταιμε Α^* και ονομάζεται προσαρτημένος πίνακας του Α. Με άλλα λόγια από το Θεώρημα 4.12 προκύπτει ότι,

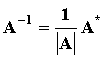
Παράδειγμα : Θα υπολογίσουμε τον αντίστροφο του πίνακα Έχουμε
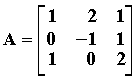
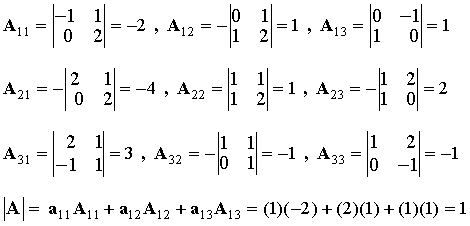
Άρα

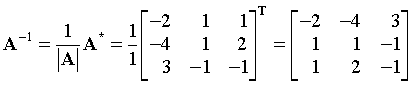
Θεώρημα 4.13 (Κανόνας του Cramer)

Έστω γραμμικό σύστημα Α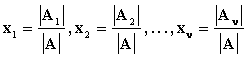 = ν εξισώσεων με ν μεταβλητές. Εάν |Α| 0, το σύστημα αυτό έχει μια και μοναδική λύση. Αυτή είναι η εξής: όπου Αi ο πίνακας που προκύπτει από τον Α, εάν αντικαταστήσουμε την i-στήλη του Α με την στήλη

Απόδειξη

Παράδειγμα :
Να αποδειχθεί ότι το γραμμικό σύστημα

x1- x2 = 1		έχει μια και μοναδική
x1 + x2 + x3 = 0		λύση, και να επιλυθεί
2x1 - x2 + 3x3 = - 2		χρησιμοποιώντας τον κανόνα του Cramer.

Απάντηση

---