Εάν Α = [αij] τριγωνικός πίνακας μεγέθους νxν, |Α| = α11α22 . . . ανν |
Θα το αποδείξουμε για πάνω τριγωνικούς πίνακες (η απόδειξη για κάτω τριγωνικούς είναι παρόμοια).
Έστω |Α| = α11α22 . . . ανν πάνω τριγωνικός πίνακας μεγέθους νxν. Προφανώς
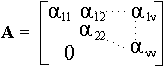
Από τον ορισμό της ορίζουσας |A| =
sgn(σ)α1σ1α2σ2 . . . ανσν όπου το άθροισμα θεωρείται πάνω σε όλες τις μεταθέσεις σ = ( σ1,σ2 , . . . ,σν ) του συνόλου Κ= {1,2, . . . ,ν }. Τώρα εάν σε μια μετάθεση σ = ( σ1,σ2 , . . . ,σν ) του Κ υπάρχει τουλάχιστον ένα στοιχείο i τέτοιο ώστε i > σi, τότε αυτό σημαίνει πως το γινόμενο sgn(σ)α1σ1α2σ2 . . . ανσν που αντιστοιχεί σ'αυτή την μετάθεση ισούται με 0, διότι αiσi = 0. Άρα οι μόνες μεταθέσεις που έχουν μη-μηδενική "συνεισφορά" στο άθροισμα είναι οι μεταθέσεις σ = ( σ1,σ2 , . . . ,σν ) του Κ για τις οποίες ισχύει : i < σi 
i = 1,2, . . . . ,ν. Επομένως |