Θεώρημα 4.11

Για κάθε τετραγωνικό πίνακα Α = [αij] μεγέθους νxν, οι παρακάτω προτάσεις είναι ισοδύναμες : (1) Ο Α είναι αντιστρέψιμος (2) Tο σύστημα Α = έχει μια και μοναδική λύση για κάθε ν (3) Tο ομογενές σύστημα Α = έχει για μόνη λύση του, την μηδενική. (4) |A| 0 (5) Ο βαθμός του πίνακα Α (ο οποίος συμβολίζεται με ρ(Α) ) ισούται με ν.

Άσκηση
a) Nα αποδειχθεί ότι οι προτάσεις (4) και (5) είναι ισοδύναμες
b) Nα αποδειχθεί ότι οι προτάσεις (3) και (5) είναι ισοδύναμες
Αποδείξεις
a) (4) (5)
Εφαρμόζουμε στον πίνακα Α, τον αλγόριθμο των Gauss-Jordan, οπότε προκύπτει ένας πίνακας Β που βρίσκεται σε απλή κλιμακωτή μορφή.
Έστω ότι Επειδή ο Β είναι τριγωνικός πίνακας από το Θεώρημα 4.8 , |B| = β₁₁β₂₂ . . . β_νν.
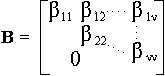
Επίσης επειδή ο Β είναι πίνακας απλής κλιμακωτής μορφής β₁₁β₂₂ . . . β_νν. 0 εάν και μόνον εάν ο Β δεν περιέχει μηδενικές γραμμές, δηλαδή από το Πόρισμα 3.1 εάν και μόνον εάν ρ(Α)=ν.
Άρα |Β| 0 ρ(Α) = ν       σχέση 4.1 Τώρα από τα θεωρήματα 4.6 και 4.9, |Α| 0 |Β| 0 διότι ο αλγόριθμος των Gauss-Jordan περιέχει μόνον στοιχειώδεις γραμμομετασχηματισμούς.
Επομένως από την σχέση 4.1 έχουμε |Α| 0 ρ(Α) = ν

b) (3) (5)
Το ομογενές γραμμικό σύστημα Α = μπορεί να γραφεί στην μορφή Από την σχέση 4.2 έχουμε:
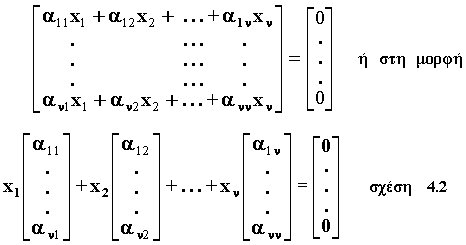
Tο Α = έχει για μόνη λύση του την μηδενική τα διανύσματα στηλών του Α είναι γραμμικώς ανεξάρτητα, δηλαδή ρ(Α) = ν .

---