1) Nα διαπιστωθεί ότι τρία επίπεδα με εξισώσεις:
αx+βy+γz = δ
α΄x+β΄y+γ΄z = δ΄
α΄΄x+β΄΄y+γ΄΄z = δ΄΄ τέμνονται σε ένα και μόνο σημείο εάν δεν μηδενίζεται η ορίζουσα των συντελεστών, εάν δηλαδή Απάντηση

---

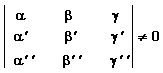
2) Να αποδειχθεί ότι τα παρακάτω συστήματα έχουν μια και μοναδική λύση. Επίσης να λυθούν με τον αλγόριθμο των Gauss-Jordan, με τον κανόνα Cramer και με αντιστροφή του πίνακα συντελεστών.

x1 - x2 + 2x3 = 1 -2x1 + 3x2 + x3 = 0 x1 - 3x2 + 4x3 = 2

x1 + 3x2 - x3 = 0 x1 + x2 + x3 = 0 x1 - x3 = 1

Απάντηση

---

3) Έστω Α πίνακας μεγέθους νxν, για τον οποίο ισχύει το εξής:
(1 γραμμή του Α) + (2 γραμμή του Α) = (3 γραμμή του Α) Μπορεί ο Α να είναι αντιστρέψιμος ;
Απάντηση

---

4) Υπό ποιές συνθήκες ο πίνακας είναι αντιστρέψιμος ; Στην συνέχεια να βρεθεί ο αντίστροφός του.
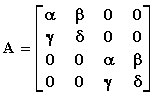
Απάντηση

---

5) Δώστε παράδειγμα πινάκων Α και Β έτσι ώστε : ο Α - Β να είναι αντιστρέψιμος ενώ οι Α , Β να μην είναι αντιστρέψιμοι.
Απάντηση

---

6) Να αποδειχθεί ο τύπος   |ΑΒ| = |Α||Β|   για πάνω τριγωνικούς πίνακες.
Απάντηση

---

7) Έστω Α πάνω τριγωνικός αντιστρέψιμος πίνακας.
Να αποδειχθεί ότι ο πίνακας Α^-1 είναι επίσης πάνω τριγωνικός.
Απάντηση

---