i) | η αποτίμηση |
ii) | το Τ είναι ικανοποιήσιμο αν και μόνον αν υπάρχει αποτίμηση που το ικανοποιεί. |
iii) | η |
iv) | η |
v) | το Τ ταυτολογικά συνεπάγεται την πρόταση |
Παρατηρούμε ότι αν Τ=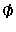 τότε
τότε 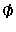

 ή
ή 
 αν η
αν η  είναι ταυτολογία. Αν το Τ δεν είναι ικανοποιήσιμο τότε Τ
είναι ταυτολογία. Αν το Τ δεν είναι ικανοποιήσιμο τότε Τ 
 για κάθε
για κάθε  . Στην περίπτωση που Τ = {
. Στην περίπτωση που Τ = {  }, γράφουμε
}, γράφουμε 

 αντί {
αντί {  }
} 
 . Tέλος αν
. Tέλος αν 

 και
και 

 τότε γράφουμε
τότε γράφουμε 

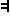
 και λέμε ότι οι προτάσεις
και λέμε ότι οι προτάσεις  και
και  είναι ταυτολογικά ισοδύναμες.
είναι ταυτολογικά ισοδύναμες.
Παραδείγματα :
1) Η πρόταση 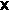 : (
: ( 
 (
( 

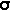 ) )
) )  ((
(( 

 )
) (
( 

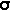 )) είναι ταυτολογία γιατί όπως βλέπουμε από τον παρακάτω πίνακα, κάθε αποτίμηση την ικανοποιεί.
)) είναι ταυτολογία γιατί όπως βλέπουμε από τον παρακάτω πίνακα, κάθε αποτίμηση την ικανοποιεί.
1.gif)
Για να είναι μια πρόταση ταυτολογία πρέπει η τελευταία στήλη του αληθοπίνακά της να αποτελείται αποκλειστικά από Α.
2) Δείξτε ότι {  1 ,
1 ,  2 }
2 } 



 1
1 
 2
2 

( 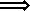 )
)
Έστω ότι {  1 ,
1 ,  2 }
2 } 
 και
και 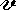 μια τυχαία αποτίμηση.
μια τυχαία αποτίμηση.
Αν  (
(  1 ) = Α και
1 ) = Α και  (
(  2 ) = Α τότε και
2 ) = Α τότε και  (
(  ) = Α και άρα
) = Α και άρα  (
(  1
1 
 2
2 
 ) = A.
) = A.
Αν είτε  (
(  1 ) = Ψ ή
1 ) = Ψ ή  (
(  2 ) = Ψ τότε
2 ) = Ψ τότε  (
(  1
1 
 2 ) = Ψ και άρα
2 ) = Ψ και άρα  (
(  1
1 
 2
2 
 ) = Α.
) = Α.
Επομένως αν {  1 ,
1 ,  2 }
2 } 
 έχουμε
έχουμε  (
(  1
1 
 2
2 
 ) = Α για κάθε αποτίμηση
) = Α για κάθε αποτίμηση 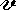 , δηλαδή
, δηλαδή 
 1
1 
 2
2 
 .
.
( 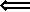 )
)
Έστω ότι 
 1
1 
 2
2 
 , και
, και 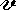 μια τυχαία αποτίμηση που ικανοποιεί το {
μια τυχαία αποτίμηση που ικανοποιεί το {  1 ,
1 ,  2 } δηλαδή
2 } δηλαδή
 (
(  1 ) =
1 ) =  (
(  2 ) = Α. Τότε όμως
2 ) = Α. Τότε όμως  (
(  ) = Α γιατί
) = Α γιατί  (
(  1
1 
 2
2 
 ) = Α.
) = Α.
Άρα {  1 ,
1 ,  2 }
2 } 
 , γιατί κάθε αποτίμηση που ικανοποιεί το {
, γιατί κάθε αποτίμηση που ικανοποιεί το {  1 ,
1 ,  2 } ικανοποιεί και τη
2 } ικανοποιεί και τη  .
.
Aσκήσεις
1) Είναι η πρόταση ( 



 )
)  ( (
( ( 


 )
) 
 ) ταυτολογία ;
) ταυτολογία ;
Απάντηση
2)Τρείς ύποπτοι συλλαμβάνονται για κάποιο έγκλημα.
O Α λέει : " Ο Β το έκανε. Ο C είναι αθώος. "
O B λέει : " Aν ο Α είναι ένοχος τότε και ο C είναι ένοχος. "
O C λέει : " Δεν το έκανα εγώ. Κάποιος από τους άλλους το έκανε. "
Είναι οι παραπάνω καταθέσεις στοιχεία ικανοποιησίμου συνόλου ; Υποθέτοντας ότι όλοι είναι αθώοι ποιός λέει ψέμματα ; Υποθέτοντας ότι η κατάθεση που είπε ο καθένας είναι αληθής, ποιός είναι αθώος και ποιός ένοχος ;
Απάντηση
Πρώτα πρέπει να τυποποιήσουμε τις καταθέσεις των τριών υπόπτων.
Θέτουμε
p : o Α είναι αθώος
q : o Β είναι αθώος και
r : o C είναι αθώος
1.gif)
O Α λέει : " Ο Β το έκανε. Ο C είναι αθώος. " |
O B λέει : " Aν ο Α είναι ένοχος τότε και ο C είναι ένοχος. " |
O C λέει : " Δεν το έκανα εγώ. Κάποιος από τους άλλους το έκανε. " |
p : o Α είναι αθώος |
q : o Β είναι αθώος και |
r : o C είναι αθώος |
O Α λοιπόν κατέθεσε | : |
O B κατέθεσε | : |
O C κατέθεσε | : r |
Θα πρέπει να μελετήσουμε το σύνολο {
Κατασκευάζουμε τον πίνακα αλήθειας για το σύνολο αυτό.
2.gif)
Βλέπουμε λοιπόν στην τρίτη γραμμή του παραπάνω αληθοπίνακα, υπάρχει αποτίμηση ( συγκεκριμένα
Άρα το σύνολο {
Αν υποθέσουμε ότι όλοι είναι αθώοι βρισκόμαστε στην πρώτη γραμμή του αληθοπίνακα, όπου
3) Αν
|
7.gif)