Ορισμός :
Μία συνάρτηση f : { Α , Ψ }k  { Α , Ψ } λέγεται συνάρτηση Boole με k μεταβλητές.
{ Α , Ψ } λέγεται συνάρτηση Boole με k μεταβλητές.
Σε κάθε συνάρτηση Boole f με k μεταβλητές αντιστοιχεί μιά πρόταση με k προτασιακές μεταβλητές που έχει τον ίδιο πίνακα αλήθειας με την f.
Ας δούμε πως βρίσκεται η πρόταση  που αντιστοιχεί σε μια συνάρτηση Boole f.
που αντιστοιχεί σε μια συνάρτηση Boole f.
Έστω f : { Α , Ψ }3  { Α , Ψ } μια συνάρτηση Boole με μεταβλητές που ορίζεται από τον "πίνακα αλήθειας".
{ Α , Ψ } μια συνάρτηση Boole με μεταβλητές που ορίζεται από τον "πίνακα αλήθειας".
1.gif)
Για να βρούμε την  που αντιστοιχεί στην f και έχει τον ίδιο πίνακα αλήθειας με την f, πρώτα προσδιορίζουμε τα στοιχεία του { Α , Ψ }3 στα οποία η f παίρνει την τιμή Α. Αυτά είναι (Α , Ψ , Ψ) , (Ψ , Α , Ψ) και (Ψ , Ψ , Α). Σε κάθε μια από αυτές τις τριάδες αντιστοιχούμε μια πρόταση στην οποία εμφανίζονται μόνο οι p1 , p2 , p3 ως εξής : Αν το πρώτο στοιχείο της τριάδας είναι Α τότε παίρνουμε την p1 , ενώ αν είναι Ψ παίρνουμε
που αντιστοιχεί στην f και έχει τον ίδιο πίνακα αλήθειας με την f, πρώτα προσδιορίζουμε τα στοιχεία του { Α , Ψ }3 στα οποία η f παίρνει την τιμή Α. Αυτά είναι (Α , Ψ , Ψ) , (Ψ , Α , Ψ) και (Ψ , Ψ , Α). Σε κάθε μια από αυτές τις τριάδες αντιστοιχούμε μια πρόταση στην οποία εμφανίζονται μόνο οι p1 , p2 , p3 ως εξής : Αν το πρώτο στοιχείο της τριάδας είναι Α τότε παίρνουμε την p1 , ενώ αν είναι Ψ παίρνουμε  p1. Όμοια για τα άλλα δύο στοιχεία της τριάδας και τελικά παίρνουμε την σύζευξη των τριών στοιχειωδών προτάσεων. Έτσι στην (Α , Ψ , Ψ) αντιστοιχεί η πρόταση p1
p1. Όμοια για τα άλλα δύο στοιχεία της τριάδας και τελικά παίρνουμε την σύζευξη των τριών στοιχειωδών προτάσεων. Έτσι στην (Α , Ψ , Ψ) αντιστοιχεί η πρόταση p1
 p2
p2
 p3. Η διάζευξη των προτάσεων που αντιστοιχούν στις τρείς τριάδες είναι η πρόταση :( p1
p3. Η διάζευξη των προτάσεων που αντιστοιχούν στις τρείς τριάδες είναι η πρόταση :( p1
 p2
p2
 p3 )
p3 ) (
(  p1
p1 p2
p2
 p3 )
p3 ) (
(  p1
p1
 p2
p2 p3 )
της οποίας ο πίνακας αλήθειας ταυτίζεται με της f.
p3 )
της οποίας ο πίνακας αλήθειας ταυτίζεται με της f.
Παράδειγμα :
1) Δίνεται η συνάρτηση Boole g με τρείς μεταβλητές, που ορίζεται από τον πίνακα:
2.gif)
Να βρεθεί η πρόταση που έχει τον ίδιο πίνακα αλήθειας με την g.
Όπως προηγούμενα παίρνουμε τις τριάδες (Α , Α , Ψ) , (Α , Ψ , Ψ) , (Ψ , Α , Α) , (Ψ , Ψ , Ψ) και κατασκευάζουμε τις προτάσεις :
p1 p2
p2
 p3 ,
p1
p3 ,
p1
 p2
p2
 p3 ,
p3 ,  p1
p1 p2
p2 p3 ,
p3 ,  p1
p1
 p2
p2
 p3
Η ζητούμενη πρόταση είναι
( p1
p3
Η ζητούμενη πρόταση είναι
( p1 p2
p2
 p3 )
p3 ) (
p1
(
p1
 p2
p2
 p3 )
p3 ) (
(  p1
p1 p2
p2 p3 )
p3 ) (
(  p1
p1
 p2
p2
 p3 )
p3 )
Παρατηρούμε ότι οι προτάσεις που αντιστοιχούν σε συναρτήσεις Boole, περιέχουν μόνο τους συνδέσμους
Ορισμός :
Μια πρόταση  είναι σε κανονική διαζευκτική μορφή αν είναι διάζευξη συζεύξεων προτασιακών μεταβλητών ή αρνήσεων προτασιακών μεταβλητών.
είναι σε κανονική διαζευκτική μορφή αν είναι διάζευξη συζεύξεων προτασιακών μεταβλητών ή αρνήσεων προτασιακών μεταβλητών.
Άμεσα φαίνεται ότι κάθε πρόταση είναι ταυτολογικά ισοδύναμη με μια άλλη σε κανονική διαζευκτική μορφή. Και αυτό γιατί κάθε πρόταση μπορεί να θεωρηθεί σαν συνάρτηση Boole.
Για παράδειγμα έστω η πρόταση p1 ( ( p2
( ( p2
 p1)
p1) p3 ), της οποίας ο πίνακας αλήθειας είναι :
p3 ), της οποίας ο πίνακας αλήθειας είναι :
3.gif)
Ο πίνακας αυτός ορίζει και μια συνάρτηση Boole με τρεις μεταβλητές, Αυτή η συνάρτηση παίρνει την τιμή Α για τις τριάδες
(A , A , A) , ( A , Ψ , A) , (Ψ , A , A) , ( Ψ, A , Ψ) , (Ψ , Ψ , A) , (Ψ , Ψ , Ψ)
Άρα η πρόταση που έχει τον ίδιο πίνακα αλήθειας με αυτήν τη συνάρτηση (και επομένως και με την αρχική πρόταση ) είναι η
( p1 p2
p2 p3 )
p3 ) ( p1
( p1
 p2
p2 p3 )
p3 ) (
( p1
p1 p2
p2 p3 )
p3 ) (
( p1
p1 p2
p2
 p3 )
p3 ) (
( p1
p1
 p2
p2 p3 )
p3 ) (
( p1
p1
 p2
p2
 p3 )
p3 )
Δηλαδή p1 ( ( p2
( ( p2
 p1)
p1) p3 )
p3 ) 
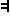 ( p1
( p1 p2
p2 p3 )
p3 ) ( p1
( p1
 p2
p2 p3 )
p3 ) (
( p1
p1 p2
p2 p3 )
p3 ) (
( p1
p1 p2
p2
 p3 )
p3 ) (
( p1
p1
 p2
p2 p3 )
p3 ) (
( p1
p1
 p2
p2
 p3 )
p3 )
Στην πρόταση p1 ( ( p2
( ( p2
 p1)
p1) p3 ) αντιστοιχεί και άλλη πρόταση σε κανονική διαζευκτική μορφή που είναι ταυτολογικά ισοδύναμη με αυτήν.
Αυτό φαίνεται παρακάτω.
p3 ) αντιστοιχεί και άλλη πρόταση σε κανονική διαζευκτική μορφή που είναι ταυτολογικά ισοδύναμη με αυτήν.
Αυτό φαίνεται παρακάτω.
Από την γνωστή ταυτολογία ( 

 )
)  (
( 


 ) έχουμε
) έχουμε 



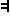



 και άρα
και άρα
p1 ( ( p2
( ( p2
 p1)
p1) p3 )
p3 ) 
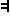
 p1
p1  ( p2
( p2
 p1)
p1) p3 αλλά η πρόταση
p3 αλλά η πρόταση  p1
p1  ( p2
( p2
 p1)
p1) p3 είναι σε κανονική διαζευκτική μορφή.
p3 είναι σε κανονική διαζευκτική μορφή.
Ασκήσεις
1) Βρείτε μια πρόταση σε κανονική διαζευκτική μορφή που είναι ταυτολογικά ισοδύναμη με την  ( p1
( p1  ( p2
( p2  p3) )
Απάντηση
p3) )
Απάντηση
2) Βρείτε μια πρόταση σε κανονική διαζευκτική μορφή που είναι ταυτολογικά ισοδύναμη με την  ( p1
( p1  p2)
p2) (
(  p1
p1 p2 )
Απάντηση
p2 )
Απάντηση
Ορισμός :
Έστω Α 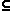 {
{  ,
,  ,
,  ,
,  ,
,  }. Το Α είναι ένα επαρκές σύνολο συνδέσμων αν κάθε πρόταση
}. Το Α είναι ένα επαρκές σύνολο συνδέσμων αν κάθε πρόταση  είναι ταυτολογικά ισοδύναμη με μια πρόταση που περιέχει μόνο συνδέσμους από το Α.
είναι ταυτολογικά ισοδύναμη με μια πρόταση που περιέχει μόνο συνδέσμους από το Α.
Το σύνολο {  ,
,  ,
,  } είναι προφανώς επαρκές γιατί για κάθε πρόταση
} είναι προφανώς επαρκές γιατί για κάθε πρόταση  μπορούμε να βρούμε μια άλλη
μπορούμε να βρούμε μια άλλη  * σε κανονική διαζευκτική μορφή με
* σε κανονική διαζευκτική μορφή με 

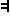
 *.
*.
Επίσης το {  ,
,  }είναι επαρκές. Αυτό , γιατί όπως προηγούμενα για κάθε
}είναι επαρκές. Αυτό , γιατί όπως προηγούμενα για κάθε  έχουμε
έχουμε 

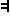
 *.
*.
Αν η  * δεν περιέχει διαζεύξεις τότε δεν χρειάζεται να δείξουμε τίποτα. Αν περιέχει διαζεύξεις τότε για κάθε διάζευξη της
* δεν περιέχει διαζεύξεις τότε δεν χρειάζεται να δείξουμε τίποτα. Αν περιέχει διαζεύξεις τότε για κάθε διάζευξη της  * εφαρμόζουμε την
* εφαρμόζουμε την 

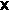

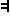
 (
( 



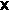 ) και τελικά βρίσκουμε μια πρόταση που περιέχει μόνο τους συνδέσμους
) και τελικά βρίσκουμε μια πρόταση που περιέχει μόνο τους συνδέσμους  και
και  .
.
Παράδειγμα :
Έστω η πρόταση p2  (
(  p1
p1 p3 ).
p3 ).
Έχουμε
p2 (
( p1
p1 p3 )
p3 ) 
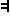
 p2
p2 (
( p1
p1 p3 )
p3 ) 
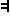
 (
(
 p2
p2
 (
(  p1
p1 p3 ) )
p3 ) ) 
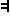

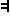
 ( p2
( p2  ( p1
( p1 
 p3 ) )
p3 ) ) 
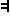
 ( p2
( p2 p1
p1
 p3 )
p3 )
Μπορούμε επίσης να δείξουμε ότι και τα σύνολα {  ,
,  } και {
} και {  ,
,  } είναι επαρκή.
} είναι επαρκή.
Για το {  ,
,  } χρειάζεται να χρησιμοποιήσουμε την ισοδυναμία
} χρειάζεται να χρησιμοποιήσουμε την ισοδυναμία 

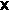

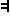
 (
( 



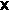 )
)
και για το {  ,
,  } την
} την 

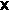

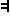



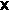 .
.
Ασκήσεις
1) Βρείτε πρόταση που να περιέχει μόνο τους συνδέσμους  ,
,  και να είναι ταυτολογικά ισοδύναμη με την
p1
και να είναι ταυτολογικά ισοδύναμη με την
p1 ( p3
( p3
 p2 )
Απάντηση
p2 )
Απάντηση
2) Όμοια με την προηγούμενη άσκηση για την πρόταση
p1 ( p2
( p2 p3 )
p3 )
Απάντηση
3) Βρείτε πρόταση που να περιέχει μόνο τους συνδέσμους  ,
,  και να είναι ταυτολογικά ισοδύναμη με την
p1
και να είναι ταυτολογικά ισοδύναμη με την
p1 (
(  p2
p2 p3 )
Απάντηση
p3 )
Απάντηση
4) Όμοια με την προηγούμενη άσκηση για την πρόταση
( p2 p1 )
p1 ) ( p1
( p1 
 p3 )
p3 )
Απάντηση
Ορίζουμε δύο καινούργιους συνδέσμους , με τους παρακάτω πίνακες αλήθειας :
4.gif) Ας δείξουμε ότι το σύνολο {
Ας δείξουμε ότι το σύνολο { 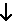 } είναι επαρκές σύνολο συνδέσμων. Επειδή το {
} είναι επαρκές σύνολο συνδέσμων. Επειδή το {  ,
,  } είναι επαρκές αρκεί να δείξουμε πως να μετασχηματίζουμε την άρνηση και την διάζευξη για να βρούμε μια πρόταση που να περιέχει μόνο τον σύνδεσμο
} είναι επαρκές αρκεί να δείξουμε πως να μετασχηματίζουμε την άρνηση και την διάζευξη για να βρούμε μια πρόταση που να περιέχει μόνο τον σύνδεσμο 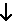 .
.
Παρατηρούμε ότι
Άρα το { 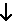 } είναι επαρκές.
} είναι επαρκές.
Παράδειγμα :
Ας βρούμε πρόταση που να περιέχει μόνο τον σύνδεσμο 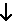 και να είναι ταυτολογικά ισοδύναμη με την p1
και να είναι ταυτολογικά ισοδύναμη με την p1 p2
p2
Έχουμε
p1 p2
p2 
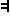
 p1
p1 p2
p2 
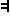 (
( p1
p1 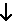 p2 )
p2 ) 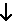 (
( p1
p1 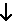 p2 )
p2 )

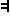 ( (p1
( (p1 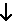 p1 )
p1 )
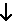 p2 )
p2 ) 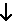 ( (p1
( (p1 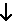 p1 )
p1 ) 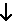 p2 )
p2 )
Μπορούμε εύκολα να δούμε επίσης ότι
και επειδή το σύνολο {  ,
,  } είναι επαρκές και το σύνολο { | } είναι επίσης επαρκές.
} είναι επαρκές και το σύνολο { | } είναι επίσης επαρκές.
Άσκηση :
Έστω ότι θέλουμε να βρούμε πρόταση που να περιέχει μόνο τον σύνδεσμο | και να είναι ταυτολογικά ισοδύναμη με την (
p1
 p2 )
p2 )  p3.
Απάντηση
p3.
Απάντηση
1.gif)
2.gif)
3.gif)
4.gif)