1 
2 
1 ( 2 )Απάντηση
(
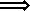)Έστω
1 2 και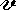 
τυχαία αποτίμηση.Αν
( 1 ) = ( 2 ) = Α τότε επειδή ( 1 2 ) = A θα έχουμε ( ) = Α.Άρα και
( 1 ( 2 ) ) = Α. Αν ( 1 ) = Ψ τότε ( 1 ( 2 ) ) = Α.Αν
( 1 ) = Α και ( 2 ) = Ψ τότε ( 2 ) =Α και ( 1 ( 2 ) ) = Α επίσης.Επομένως η
1 ( 2 ) είναι ταυτολογία.(
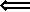)Έστω
1 ( 2 ) και 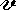τυχαία αποτίμηση.Αν
( 1 ) = Ψ τότε ( 1 2 ) = Ψ άρα και
( 1 2 ) = Α.Αν
( 1 ) = Α και ( 2 ) = Ψ τότε επίσης ( 1 2 ) = Ψ και
( 1 2 ) = Α.Αν
( 1 ) = ( 2 ) = Α τότε επειδή ( 1 ( 2 ) ) = A ( γιατί 1 ( 2 ) ) θα πρέπει και ( ) = Α. Επομένως ( 1 2 ) = Α. Άρα γενικά η 1 2 είναι ταυτολογία.
Επιστροφή |