Απαντήσεις στις Ασκήσεις 4ου Κεφαλαίου

1) Nα διαπιστωθεί ότι τρία επίπεδα με εξισώσεις:
αx+βy+γz = δ
α΄x+β΄y+γ΄z = δ΄
α΄΄x+β΄΄y+γ΄΄z = δ΄΄ τέμνονται σε ένα και μόνο σημείο εάν δεν μηδενίζεται η ορίζουσα των συντελεστών, εάν δηλαδή Απάντηση
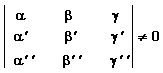
Οι εξισώσεις των τριών επιπέδων αποτελούν ένα γραμμικό σύστημα με τρείς εξισώσεις και τρείς μεταβλητές. Εάν τα επίπεδα τέμνονται σε ένα μόνο σημείο τότε οι συντεταγμένες μόνον αυτού του σημείου θα επαληθεύουν το σύστημα. Δηλαδή το σύστημα θα πρέπει να έχει μια και μοναδική λύση. Σύμφωνα με το Θεώρημα 4.13 για να έχει μια και μοναδική λύση θα πρέπει η ορίζουσα των συντελεστών να είναι διάφορη του μηδενός.

---

2) Να αποδειχθεί ότι τα παρακάτω συστήματα έχουν μια και μοναδική λύση. Επίσης να λυθούν με τον αλγόριθμο των Gauss-Jordan, με τον κανόνα Cramer και με αντιστροφή του πίνακα συντελεστών.

x1 - x2 + 2x3 = 1 -2x1 + 3x2 + x3 = 0 x1 - 3x2 + 4x3 = 2

x1 + 3x2 - x3 = 0 x1 + x2 + x3 = 0 x1 - x3 = 1

Απάντηση
Οι ορίζουσες των συντελεστών των αγνώστων για τα δύο συστήματα είναι: Σύμφωνα με το Θεώρημα 4.13 το κάθε σύστημα έχει μια και μοναδική λύση διότι η αντίστοιχη ορίζουσα είναι διάφορη του μηδενός. Εφαρμόζουμε τον αλγόριθμο Gauss-Jordan για την λύση του πρώτου συστήματος. Ο επαυξημένος πίνακας που σημαίνει ότι x₁ = 1/12 , x₂ = -1/12 , x₃ = 5/12
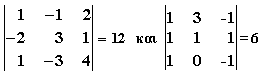
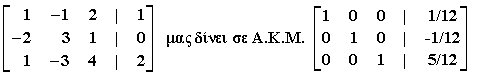
Ο κανόνας Cramer δίνει Σύμφωνα με το Θεώρημα 4.12 υπάρχει ο αντίστροφος πίνακας των συντελεστών διότι η αντίστοιχη ορίζουσα είναι μη μηδενική. Το Θεώρημα 4.12 δίνει και την διαδικασία ευρέσεως του αντίστροφου πίνακα. Γράφοντας το σύστημα στην μορφή Α = και πολλαπλασιάζοντας από αριστερά με τον αντίστροφο πίνακα έχουμε την λύση του συστήματος Ανάλογα έχουμε και για το δεύτερο σύστημα

---

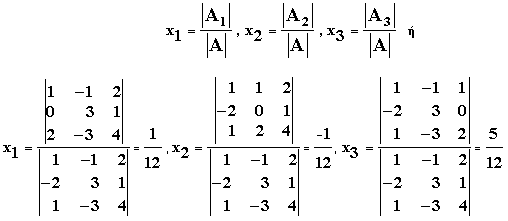
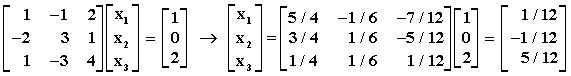
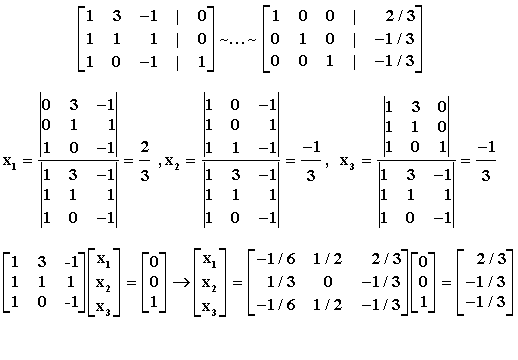
3) Έστω Α πίνακας μεγέθους νxν, για τον οποίο ισχύει το εξής:
(1 γραμμή του Α) + (2 γραμμή του Α) = (3 γραμμή του Α) Μπορεί ο Α να είναι αντιστρέψιμος ;
Απάντηση
Σύμφωνα με το Θεώρημα 4.9(ii) αν στην ορίζουσα του πίνακα Α προσθέσουμε την 1 γραμμή στην 2 γραμμή, η τιμή της ορίζουσας παραμένει η ίδια. Μετά από την πρόσθεση η 2 γραμμή θα είναι ίδια με την 3 γραμμή, που σημαίνει λόγω του Θεωρήματος 4.7 ότι |Α| = 0. Επομένως ο Α δεν είναι αντιστρέψιμος διότι πρέπει να έχει ορίζουσα μη μηδενική (Θεώρημα 4.12)

---

4) Υπό ποιές συνθήκες ο πίνακας είναι αντιστρέψιμος ; Στην συνέχεια να βρεθεί ο αντίστροφός του.
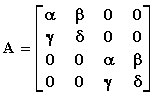
Απάντηση
Βρίσκουμε την ορίζουσα του πίνακα που είναι Για να είναι αντιστρέψιμος ο πίνακας θα πρέπει η αντίστοιχη ορίζουσα να είναι μη μηδενική δηλαδή ( αδ - βγ )² 0.
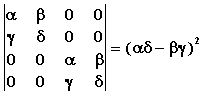
Εάν πληρούται η συνθήκη ( αδ - βγ )² 0 τότε υπάρχει ο αντίστροφος και είναι ο

---

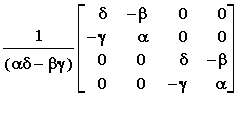
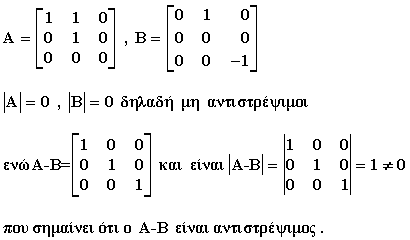
5) Δώστε παράδειγμα πινάκων Α και Β έτσι ώστε : ο Α - Β να είναι αντιστρέψιμος ενώ οι Α , Β να μην είναι αντιστρέψιμοι.
Απάντηση

---

6) Να αποδειχθεί ο τύπος   |ΑΒ| = |Α||Β|   για πάνω τριγωνικούς πίνακες.
Απάντηση
Ο πίνακας (μεγέθους νxν ) Α=[a_ij] με a_ij = 0 για όλα τα ζεύγη (i,j) με i > j .
Ο πίνακας (μεγέθους νxν ) B=[b_ij] με b_ij = 0 για όλα τα ζεύγη (i,j) με i > j .
To γινόμενο ΑΒ=[c_ij] με c_ij=a_i1b_1j + a_i2b_2j + . . . + a_ivb_vj είναι μεγέθους νxν.
Στον πίνακα ΑΒ τα στοιχεία c_ij για τα οποία είναι i > j είναι c_ij = 0 διότι ο κάθε όρος του αθροίσματος a_i1b_1j + a_i2b_2j + . . . + a_ivb_vj όταν i > j θα έχει τουλάχιστον έναν από τους παράγοντες των γινομένων a_irb_rj ( r = 1, 2 , ... ,ν ) ίσο με μηδέν.
Επομένως ο ΑΒ είναι πάνω τριγωνικός.
Τα στοιχεία (c₁₁ , c₂₂ , . . . , c_νν ) της διαγωνίου του ΑΒ είναι c_ii=a_i1b_1i + a_i2b_2i + . . . + a_iib_ii + . . . + a_ivb_vi = a_iib_ii με i =1 , . . . ,ν Επομένως ο πίνακας ΑΒ έχει ως στοιχεία της διαγωνίου του τα a₁₁b₁₁ , a₂₂b₂₂ , . . . , a_iib_ii , . . . , a_ννb_νν και σύμφωνα με το Θεώρημα 4.8 επειδή ο ΑΒ είναι τριγωνικός |ΑΒ| = a₁₁b₁₁a₂₂b₂₂ . . . a_ννb_νν = ( a₁₁ a₂₂ . . . a_νν )( b₁₁b₂₂ . . . b_νν ) = |Α||Β|

---

7) Έστω Α πάνω τριγωνικός αντιστρέψιμος πίνακας.
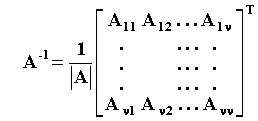
Να αποδειχθεί ότι ο πίνακας Α^-1 είναι επίσης πάνω τριγωνικός.
Απάντηση
Έστω πάνω τριγωνικός πίνακας Α = [α_ij] μεγέθους νxν με α_ij = 0 για όλα τα ζεύγη (i,j) με i > j. Είναι |Α| 0 διότι ο Α είναι αντιστρέψιμος και γενικώς έχουμε Οι συμπαράγοντες Α_ij των στοιχείων α_ij με i < j του πάνω τριγωνικού πίνακα Α είναι όλοι μηδέν διότι κάθε συμπαράγοντας Α_ij = (-1)^i+j|M_ij| όπου |M_ij| είναι η ελάσσων ορίζουσα του πάνω τριγωνικού πίνακα M_ij μεγέθους (ν-1)x(ν-1) που προκύπτει από τον Α εάν αφαιρεθούν i-γραμμή και j-στήλη. Όμως ο πίνακας M_ij ως τριγωνικός θα έχει ορίζουσα ίση με το γινόμενο των στοιχείων της διαγωνίου του ( Θεώρημα 4.8 ). Η διαγώνιος του M_ij αποτελείται μέχρι και το στοιχείο της θέσης (i-1,j-1) από τα στοιχεία ( α₁₁ , α₂₂ , . . . , α_(i-1)(j-1) ) δηλαδή τα ίδια τα στοιχεία του Α. Με την αφαίρεση της i-γραμμής αφαιρείται και το α_ii στοιχείο της διαγωνίου του Α και στον πίνακα M_ij που προέκυψε, στην θέση (i,i) θα είναι το στοιχείο α_(i+1)i του πίνακα Α, που είναι όμως μηδενικό. Επομένως |M_ij| = 0 για όλα τα ζεύγη (i,j) με i < j . Καθώς ο πίνακας των συμπαραγόντων είναι κάτω τριγωνικός , ο ανάστροφός του θα είναι πάνω τριγωνικός. Άρα και ο Α^-1 θα είναι πάνω τριγωνικός.

---