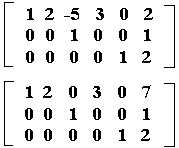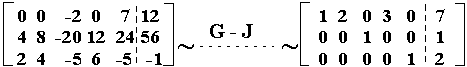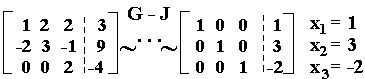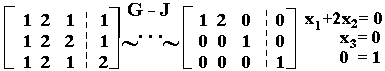Κεφάλαιο 1
Γραμμικά συστήματα

1.1:Βασικοί ορισμοί

Γραμμική εξίσωση με ν μεταβλητές :
Κάθε εξίσωση της μορφής a₁x₁+a₂x₂+. . . +a_νx_ν=b όπου a₁,a₂, . . .,a_ν, b εR
Λύση της γραμμικής εξίσωσης a₁x₁+a₂x₂+. . .+a_νx_ν=b :
Μια ακολουθία ν αριθμών s₁,s₂, . . . ,s_ν η οποία ικανοποιεί την εξίσωση εάν θέσουμε x₁=s₁, x₂=s₂, . . . , x_ν=s_ν .
Σύστημα γραμμικών εξισώσεων ή γραμμικό σύστημα :
Κάθε πεπερασμένο σύνολο εξισώσεων με ν μεταβλητές.

Λύση γραμμικού συστήματος :
Μια ακολουθία ν αριθμών s₁,s₂, . . . ,s_ν , η οποία είναι λύση για κάθε εξίσωση του συστήματος
π.χ.  α) Το γραμμικό σύστημα

4x1-x2+3x3 = -1

3x1+x2+9x3= -4 έχει για λύση του, την  x1=1, x2 =2, x3= -1.

β) Το γραμμικό σύστημα

x1+ x2 = 4

2x1+2x2 = 6  δεν έχει λύσεις.

Συμβατό γραμμικό σύστημα : Γραμμικό σύστημα που έχει τουλάχιστον μια λύση.

Μη-συμβατό γραμμικό σύστημα : Γραμμικό σύστημα που δεν έχει καμμία λύση.

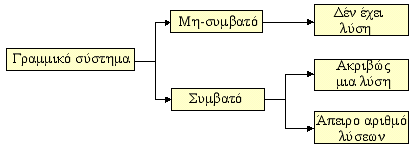
Θεώρημα 1.1 :

Κάθε γραμμικό σύστημα  έχει ακριβώς μια λύση ή άπειρο αριθμό λύσεων ή καμμία λύση.

Άσκηση : Αποδείξτε το Θεώρημα 1.1 για γραμμικά συστήματα 2 εξισώσεων με 2 μεταβλητές. Απόδειξη

Γενικά ένα γραμμικό σύστημα m εξισώσεων με n μεταβλητές θα έχει την μορφή:

a11x1+a12x2+ . . . +a1nxn= b1

a21x1+a22x2+ . . . +a2nxn= b2

.                 .                 .             .                 .                 .             .                 .                 .

am1x1+am2x2+. . .+amnxn= bm

ο πίνακας : ονομάζεται επαυξημένος πίνακας του παραπάνω γραμμικού συστήματος.

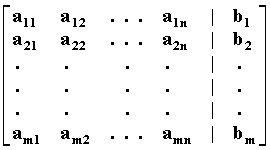
Στην συνέχεια θα αναφέρουμε κάποια θέματα που έχουν σχέση με τους
πίνακες και είναι χρήσιμα στην επίλυση των γραμμικών συστημάτων.

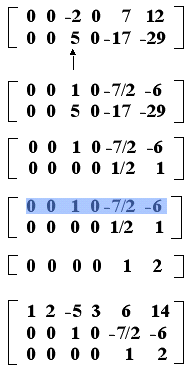
Στοιχειώδη πράξη ή στοιχειώδη γραμμομετασχηματισμό σ'ένα πίνακα ονομάζουμε κάθε διαδικασία που ανήκει σε μια από τις 3 παρακάτω κατηγορίες:

Ορισμός:
Εάν ένας πίνακας Β προκύπτει από τον πίνακα Α κατόπιν κάποιων στοιχειωδών γραμμομετασχηματισμών τότε θα λέμε ότι ο πίνακας Β είναι γραμμοϊσοδύναμος του Α και αυτό συμβολίζεται με Α ~ Β.

Παρατηρήσεις
(1) Κάθε στοιχειώδης γραμμομετασχηματισμός είναι αντιστρέψιμος.
(2) Η σχέση ~ είναι συμμετρική ( δηλ. εάν Α ~ Β τότε Β ~ Α ).

Ορισμός:
Ένας πίνακας θα λέμε ότι βρίσκεται σε απλή κλιμακωτή μορφή ( Α.Κ.Μ.) εάν έχει τα εξής χαρακτηριστικά :

(1) Εάν υπάρχουν μηδενικές γραμμές , αυτές είναι οι τελευταίες γραμμές του πίνακα .

(2) Εάν μια γραμμή περιέχει τουλάχιστον ένα μη-μηδενικό στοιχείο, τότε το πρώτο της μη-μηδενικό στοιχείο είναι το 1 ( βασικό 1 ) .

(3) Για κάθε ζεύγος γειτονικών γραμμών i και i+1 το βασικό 1 της i+1 θα βρίσκεται δεξιότερα του βασικού 1 της i .

(4) Κάθε στήλη , η οποία περιέχει κάποιο βασικό 1, θα έχει σ'όλες τις άλλες θέσεις μηδενικά .

π.χ.

1.2: Αλγόριθμος των Gauss-Jordan

Αλγόριθμος των Gauss-Jordan

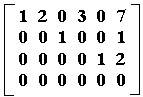
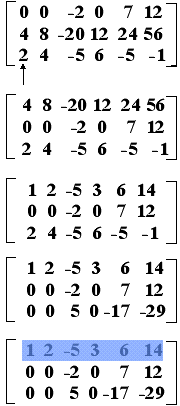Βήμα 1 Εντοπίζουμε την αριστερότερη στήλη που περιέχει τουλάχιστον ένα μη-μηδενικό στοιχείο.



Βήμα 2 Εάν το πρώτο στοιχείο της στήλης του βήματος 1 είναι 0, τότε εναλλάσουμε την πρώτη γραμμή με κάποια άλλη έτσι ώστε το πρώτο στοιχείο της παραπάνω στήλης να γίνει διάφορο του μηδενός.

Βήμα 3 Εάν τώρα μετά το βήμα 2, το πρώτο στοιχείο της στήλης του βήματος 1 είναι a, τότε πολλαπλασιάζουμε την πρώτη γραμμή με 1/a (Δημιουργούμε βασικό 1)

Βήμα 4 Προσθέτουμε πολλαπλάσια της πρώτης γραμμής στις άλλες γραμμές έτσι ώστε να προκύψουν μηδενικά στοιχεία κάτω από το βασικό 1.

Βήμα 5 Καλύπτουμε την πρώτη γραμμή και εφαρμόζουμε τα βήματα 1-5 στον υποπίνακα που προκύπτει.

 

 

 

 

 

 

Βήμα 6 Ξεκινώντας από την τελευταία γραμμή που περιέχει τουλάχιστον ένα μη-μηδενικό στοιχείο και προχωρώντας προς τα πάνω προσθέτουμε πολλαπλάσια της κάθε γραμμής στις πιο πάνω γραμμές έτσι ώστε να προκύψουν μηδενικά πάνω από κάθε βασικό 1.

 

 

1.3: Επίλυση Γραμμικών συστημάτων

Θεώρημα 1.2 :

Εάν οι επαυξημένοι πίνακες δύο γραμμικών συστημάτων είναι γραμμοϊσοδύναμοι, τότε αυτά έχουν τις ίδιες λύσεις.

π.χ.

-2x3 +7x5 = 12 2x1 +4x2 -10x3 +6x4+12x5 = 28 2x1 +4x2 -5x3 +6x4-5x5 = -1

x1 +2x2 +3x4 = 7 x3 = 1 x5 = 2

x1 = 7-2s-3t x2 = s x3 = 1 x4 = t x5 = 2

δηλ. τα παραπάνω δύο συστήματα έχουν τις ίδιες λύσεις.

Παρατήρηση:
Εάν ο επαυξημένος πίνακας ενός γραμμικού συστήματος βρίσκεται σε Απλή Κλιμακωτή Μορφή τότε ο προσδιορισμός των λύσεών του είναι προφανής.

Το Θεώρημα 1.2 και η παρατήρηση που το ακολουθεί μας παρέχουν ένα συστηματικό τρόπο επίλυσης των γραμμικών συστημάτων. Συγκεκριμένα βρίσκουμε τον επαυξημένο πίνακα του γραμμικού συστήματος και τον μετατρέπουμε σε πίνακα Α.Κ.Μ. χρησιμοποιώντας τον αλγόριθμο των Gauss-Jordan.
Ο πίνακας Α.Κ.Μ. είναι προφανώς γραμμοϊσοδύναμος με τον αρχικό, διότι ο αλγόριθμος περιέχει στοιχειώδεις γραμμομετασχηματισμούς. Βρίσκουμε το γραμμικό σύστημα που έχει για επαυξημένο πίνακα τον πίνακα Α.Κ.Μ. και το οποίο έχει ακριβώς τις ίδιες λύσεις με το αρχικό. Ο προσδιορισμός των λύσεων αυτού του συστήματος είναι προφανής.

Παραδείγματα :

x1 +2x2+2x3 = 3 -2x1 +3x2-x3 = 9 2x3 = -4
x1 +2x2 + x3 = 1 x1 +2x2+2x3 = 1 x1 +2x2+2x3 = 2

Παρατηρήσεις:
Έστω γραμμικό σύστημα , m εξισώσεων με n μεταβλητές, του οποίου ο επαυξημένος πίνακας βρίσκεται σε απλή κλιμακωτή μορφή (Α.Κ.Μ.)

(1) Θα ονομάζουμε :
     (α) Βασικές μεταβλητές του: Μεταβλητές που αντιστοιχούν στα βασικά 1
     (β) Ελεύθερες μεταβλητές του: Μεταβλητές που δεν είναι βασικές
     (γ) Βασικές εξισώσεις του:Εξισώσεις που έχουν μεταβλητές στο αριστερό μέρος
     (δ) Απαλοίφουσες εξισώσεις του: Εξισώσεις που δεν είναι βασικές
     (ε) Βαθμός ή τάξη του συστήματος: Ο αριθμός (ρ) των βασικών του εξισώσεων. Είναι ρ < m , n .
(2) Το σύστημα είναι συμβατό εάν και μόνον εάν ικανοποιούνται όλες οι απαλοίφουσες εξισώσεις του.
(3) Αν το σύστημα είναι συμβατό και ρ = n , τότε έχει ακριβώς μια λύση.
(4) Αν το σύστημα είναι συμβατό και ρ < n , τότε έχει άπειρο αριθμό λύσεων (παραμετρική λύση ).
(5) Αν m < n τότε το σύστημα αποκλείεται να έχει ακριβώς μια λύση.

1.4 : Ομογενή γραμμικά συστήματα

Γραμμικά συστήματα της μορφής

a11x1+a12x2+ . . . +a1nxn= 0

a21x1+a22x2+ . . . +a2nxn= 0

.                 .                 .             .                 .                 .             .                 .                 .

am1x1+am2x2+. . .+amnxn= 0

Όλα τα ομογενή γραμμικά συστήματα είναι προφανώς συμβατά.

---