Απαντήσεις Ασκήσεων 3ου Κεφαλαίου

1) Για καθένα από τους παρακάτω πίνακες να επαληθευτεί ότι η διάσταση του γραμμοχώρου του ισούται με την διάσταση του στηλοχώρου του.
Απάντηση :
Ο πίνακας (i) σε Α.Κ.Μ. δίνει
και σύμφωνα με το Θεώρημα 3.1 και το Θεώρημα 3.2 έχουμε ότι η διάσταση του γραμμοχώρου του είναι δύο.
Αν πάρουμε τον ανάστροφο του πίνακα (i) και τον φέρουμε σε Α.Κ.Μ. θα βρούμε
οπότε η διάσταση του στηλοχώρου του αρχικού πίνακα είναι πάλι δύο.
Το αποτέλεσμα αυτό είναι μια επαλήθευση του Θεωρήματος 3.3
Aνάλογα για τον πίνακα (ii) έχουμε :
όπου φαίνεται όπως και προηγουμένως ότι οι διαστάσεις στηλοχώρου και γραμμοχώρου είναι τρία.
2) Κατασκευάστε έναν πίνακα του οποίου ο γραμμοχώρος περιέχει τα διανύσματα (1,1) , (1,2) ενώ ο στηλοχώρος τα διανύσματα (1,0,0) , (0,0,1).
Απάντηση :
Τα δοθέντα διανύσματα (1,0,0) και (0,0,1) είναι γραμμικώς ανεξάρτητα όπως είναι και τα (1,1) , (1,2). Σχηματίζουμε ένα πίνακα που έχει τα διανύσματα (1,0,0) και (0,0,1) ως στήλες. Ο στηλοχώρος αυτού του πίνακα περιέχει τα (1,0,0) και (0,0,1). Προσθέτουμε την τρίτη γραμμή στην πρώτη και κατόπιν την πρώτη στην τρίτη. Τότε παρουσιάζονται στις γραμμές του πίνακα τα δύο διανύσματα (1,1) , (1,2) δηλαδή ο γραμμοχώρος του πίνακα περιέχει και τα (1,1) , (1,2). .

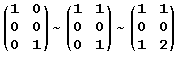
3) Έστω πίνακας Α μεγέθους mxn , όπου m n. Nα αποδειχθεί ότι: Τα διανύσματα γραμμών του Α ή τα διανύσματα στηλών του Α είναι γραμμικώς εξαρτημένα.
Απάντηση :
Μεταξύ των m και n το ένα θα είναι μεγαλύτερο από το άλλο, χωρίς να επιρρεάζεται η γενικότητα μπορούμε να υποθέσουμε ότι m μεγαλύτερο από n.
Τότε σύμφωνα με το Θεώρημα 3.3 θα είναι ρ(Α) < n < m. Το τελευταίο όμως σημαίνει ότι το πλήθος των διανυσμάτων γραμμών είναι μεγαλύτερο από τον βαθμό του πίνακα Α. Επομένως όλα τα διανύσματα γραμμές δεν μπορούν να είναι γραμμικώς ανεξάρτητα διότι τότε το ρ(Α) θα ήταν ίσο με m που είναι άτοπο. Συμπέρασμα τα m διανύσματα γραμμές είναι γραμμικώς εξαρτημένα. Ανάλογο συμπέρασμα θα έχουμε εάν είναι n μεγαλύτερο από m.

4) Εάν , να βρεθεί μια βάση και μια ορθοκανονική βάση για τον υπόχωρο των διανυσμάτων για τα οποία είναι συμβατό το γραμμικό σύστημα
Α = .
Απάντηση :

5) Δίνεται το ομογενές γραμμικό σύστημα :

2x1 -

x2 +

x3 -

x4

= 0

x1 +

x2 -

x3 +

2x4

= 0

x1 -

2x2 +

2x3 -

3x4

= 0
Να βρεθεί η διάσταση και μια βάση για τον υπόχωρο V ( του 4 ) των λύσεων του.
Απάντηση :
Φέρνουμε τον πίνακα των συντελεστών των αγνώστων σε Α.Κ.Μ.
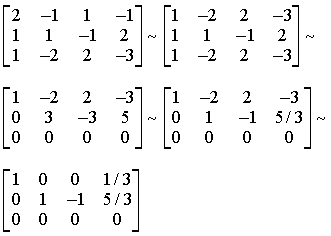
Ο πίνακας είναι βαθμού ρ = 2 και σύμφωνα με το Θεώρημα 3.5 τα διανύσματα που είναι λύσεις του συστήματος σχηματίζουν υπόχωρο διαστάσεως 4-2 = 2.
Έχουμε για

x3 = 1 , x4 = 3 το διάνυσμα λύσης (-1,-4,1,3)
x3 = 0 , x4 = 3 τo διάνυσμα λύσης (-1,-5,0,3)

Tα δύο διανύσματα { (-1,-4,1,3) , (-1,-5,0,3) } είναι γραμμικώς ανεξάρτητα και αποτελούν βάση του υπόχωρου V των λύσεων του συστήματος.
6) Έστω πίνακας Α μεγέθους 23 x 15 και βαθμού 10. Ποιός είναι ο μέγιστος αριθμός γραμμικώς ανεξαρτήτων διανυσμάτων που ικανοποιούν το ομογενές σύστημα
ΑΤ = ;
Απάντηση :
Ο πίνακας ΑΤ του συστήματος είναι μεγέθους 15 x 23 και βαθμού 10. Επομένως βάσει του Θεωρήματος 3.5 τα διανύσματα που είναι λύσεις του συστήματος σχηματίζουν υπόχωρο διαστάσεως 23 - 10 = 13. Άρα ο μέγιστος αριθμός γραμμικώς ανεξαρτήτων διανυσμάτων που ικανοποιούν το σύστημα είναι 13 όσο και η διάσταση του υπόχωρου των λύσεων.
7) Να λυθεί το παρακάτω συμβατό γραμμικό σύστημα ,

x1 -

x2 +

x3 +

x4

= 1

x1 -

x2 +

0x3 -

x4

= -1

2x1 -

2x2 +

x3 +

0x4

= 0

x1 +

x2 +

x3 +

x4

= 1

χρησιμοποιώντας το Θεώρημα 3.6 .
Απάντηση :
Σύμφωνα με το Θεώρημα 3.6 χρειαζόμαστε μια λύση του συστήματος και τον υπόχωρο των λύσεων του αντιστοίχου ομογενούς συστήματος. Για το ομογενές σύστημα φέρνωντας τον πίνακα των συντελεστών των αγνώστων σε Α.Κ.Μ. έχουμε :
Οπότε έχουμε ότι ο βαθμός του πίνακα είναι 3 άρα ο υπόχωρος των λύσεων V του ομογενούς έχει διάσταση 4-3 = 1 και το διάνυσμα π.χ. ( 1 , 0 , -2 , 1 ) είναι η βάση των λύσεων του αντιστοίχου ομογενούς συστήματος δηλαδή βάση του υπόχωρου V. Μια λύση του μη ομογενούς συστήματος είναι το διάνυσμα (-1,2,0,0) που επαληθεύει το αρχικό σύστημα.. Οπότε βάσει του Θεωρήματος 3.6 η γενική λύση του μη ομογενούς συστήματος είναι τα διανύσματα
= (-1,2,0,0) + ( t , 0 -2t , t) με το t