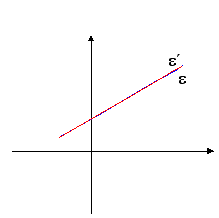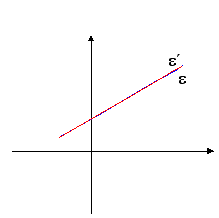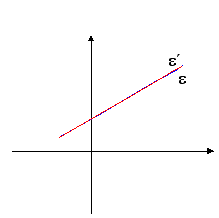Το παρακάτω γραμμικό σύστημα έχει ακριβώς μια λύση ή καμμία λύση ή άπειρο αριθμό λύσεων
a₁x+b₁y=c₁
a₂x+b₂y=c₂

Απόδειξη αλγεβρική
Εάν οι συντελεστές a₁ , b₁ είναι και οι δύο μηδέν τότε η πρώτη εξίσωση του συστήματος θα ήταν 0=c₁. Και αν το c₁ είναι διάφορο του μηδενός το σύστημα είναι μη-συμβατό ( δηλαδή χωρίς λύση ). Αν και το c₁=0 τότε το σύστημα αποτελείται μόνο από την δεύτερη εξίσωση a₂x+b₂y=c₂. Σ'αυτήν την περίπτωση το αρχικό σύστημα θα έχει άπειρες λύσεις εκτός εάν και εδώ οι συντελεστές των αγνώστων είναι μηδέν και ο σταθερός όρος διάφορος του μηδενός που δίνει πάλι μη-συμβατό σύστημα.
Έστω a₁ διάφορο του μηδενός , λύνοντας ως προς x έχουμε x=-(b₁/a₁)y+c₁/a₁. Με αντικατάσταση στην δεύτερη εξίσωση έχουμε : (a₁b₂-a₂b₁)y=(a₁c₂-c₁a₂). Εάν τώρα (a₁b₂-a₂b₁) είναι διάφορο του μηδενός έχουμε μια μόνο τιμή για το y από την οποία βρίσκουμε αντικαθιστώντας παραπάνω και μια μόνο τιμή για το x. Άρα το αρχικό σύστημα έχει μια μόνο λύση. Εάν τώρα είναι (a₁b₂-a₂b₁)=0 τότε με (a₁c₂-c₁a₂)=0 έχουμε άπειρες λύσεις για το y (διότι 0y=0) οπότε και για το x, δηλαδή το αρχικό σύστημα έχει άπειρες λύσεις. Με (a₁b₂-a₂b₁)=0 και με (a₁c₂-c₁a₂) όχι μηδέν δεν έχουμε καμμία λύση για το y και συνεπώς ούτε το αρχικό σύστημα έχει λύση. Σε όλες τις περιπτώσεις το σύστημα ή θα έχει μια λύση ακριβώς ή καμμία λύση ή άπειρες λύσεις.

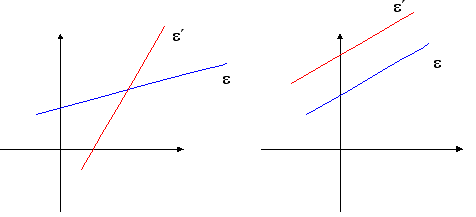
Στην περίπτωση που υπάρχει η γραφική παράσταση και των δύο εξισώσεων έχουμε :
Απόδειξη γεωμετρική
Κάθε εξίσωση του συστήματος έχει ως γραφική της παράσταση μια ευθεία.
Αυτές οι δύο ευθείες ή θα τέμνονται (μια μόνο λύση) ή θα είναι παράλληλες (καμμία λύση) ή θα ταυτίζονται (άπειρες λύσεις).