Εάν ν θετικός ακέραιος , θεωρούμε το σύνολο όλων των διατεταγμένων ν-άδων πραγματικών αριθμών ( a1,a2, . . .,aν ). Κάθε στοιχείο αυτού του συνόλου το συμβολίζουμε με
Σ'αυτό το σύνολο ορίζουμε τις εξής δύο πράξεις:
(α) Πρόσθεση διανυσμάτων
Εάν
(β) Πολλαπλασιασμός διανύσματος με αριθμό
Εάν
τότε λ
Οι πράξεις αυτές έχουν όλες τις γνωστές ιδιότητες που ισχύουν για τις αντίστοιχες πράξεις μεταξύ διανυσμάτων του επιπέδου και του χώρου .
Συγκεκριμένα :
| , | ||
| , | ||
| λ(μ | , | (λ+μ) |
| λ( | , | 1 |
Το σύνολο των διανυσμάτων , που ορίσαμε προηγουμένως , εφοδιασμένο με τις δύο πράξεις και τις αντίστοιχες ιδιότητές τους, το ονομάζουμε ν-διανυσματικό χώρο και το συμβολίζουμε με |
Στο σύνολο αυτό μπορούμε να ορίσουμε επιπλέον και το παρακάτω γινόμενο:
Εάν 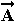 =( a1,a2, . . .,aν ) και
=( a1,a2, . . .,aν ) και 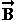 =( b1,b2, . . .,bν ) τότε
=( b1,b2, . . .,bν ) τότε
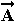

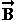 = ( a1,a2, . . .,aν )
= ( a1,a2, . . .,aν ) ( b1,b2, . . .,bν ) = a1b1 + a2b2 + . . . + aνbν
( b1,b2, . . .,bν ) = a1b1 + a2b2 + . . . + aνbν
Το γινόμενο αυτό ονομάζεται εσωτερικό γινόμενο μεταξύ των δύο διανυσμάτων.
Το εσωτερικό γινόμενο έχει όλες τις γνωστές ιδιότητες που έχει η αντίστοιχη πράξη μεταξύ διανυσμάτων του επιπέδου και του χώρου.
Συγκεκριμένα :
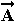

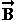 =
=
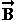

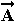
, λ(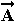

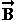 ) =
(λ
) =
(λ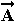

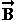 ) =
(
) =
(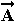
 λ
λ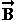 )
)
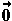

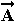 = 0
= 0 , 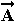
 (
(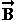 +
+ 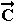 ) =
) =
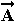

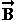 +
+ 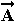

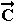
Το μήκος ή η νόρμα ενός διανύσματος 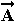 =( a1,a2, . . .,aν ) συμβολίζεται με |
=( a1,a2, . . .,aν ) συμβολίζεται με |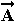 | και ορίζεται ως εξής :
| και ορίζεται ως εξής :
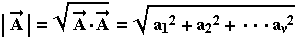
Θα λέμε ότι δύο διανύσματα 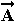 και
και 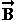 είναι ορθογώνια ή κάθετα μεταξύ τους , αν μηδενίζεται το εσωτερικό τους γινόμενο , δηλαδή εάν
είναι ορθογώνια ή κάθετα μεταξύ τους , αν μηδενίζεται το εσωτερικό τους γινόμενο , δηλαδή εάν 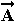

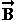 = 0.
= 0.
Επίσης θα λέμε ότι ένα διάνυσμα 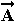 είναι μοναδιαίο αν έχει μήκος 1,
είναι μοναδιαίο αν έχει μήκος 1,
δηλαδή αν 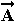

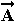 = 1.
= 1.
Τα μοναδιαία διανύσματα συνήθως τα συμβολίζουμε με 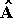 ,
, 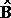 , . . .
, . . .
Παρατήρηση :
Εάν 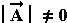 , το διάνυσμα
, το διάνυσμα 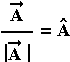 είναι μοναδιαίο.
είναι μοναδιαίο.
Αναφέρουμε ειδικά τα διανύσματα :
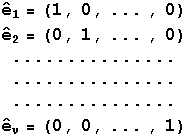
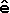 i έχει την i-συντεταγμένη ίση με 1 και όλες τις άλλες μηδενικές .
i έχει την i-συντεταγμένη ίση με 1 και όλες τις άλλες μηδενικές .
Τα διανύσματα αυτά είναι μοναδιαία και ανά δύο ορθογώνια μεταξύ τους.
Επίσης κάθε διάνυσμα 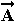 =( a1,a2, . . .,aν ) μπορεί να γραφεί στη μορφή
=( a1,a2, . . .,aν ) μπορεί να γραφεί στη μορφή 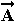 = a1
= a1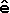 1 + a2
1 + a2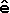 2 + . . .+ aν
2 + . . .+ aν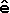 ν = a1(1,0,...,0) + a2(0,1,...,0) +. . .+ aν(0,0,...,1)
ν = a1(1,0,...,0) + a2(0,1,...,0) +. . .+ aν(0,0,...,1)
Γενικώτερα, αν  1 ,
1 ,  2 , . . . ,
2 , . . . ,  k είναι διανύσματα του
k είναι διανύσματα του 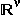 , κάθε διάνυσμα
, κάθε διάνυσμα  που γράφεται στη μορφή
που γράφεται στη μορφή
 = t1
= t1 1 + t2
1 + t2 2 + . . . + tk
2 + . . . + tk k
k
για κάποιους πραγματικούς αριθμούς t1 , t2 , ... , tk , λέμε ότι είναι γραμμικός συνδυασμός των  1 ,
1 ,  2 , ... ,
2 , ... ,  k .
k .
Εάν  ,
, 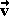 διανύσματα του
διανύσματα του 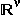 , το διάνυσμα
, το διάνυσμα
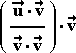
 πάνω στο
πάνω στο 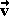 και συμβολίζεται με pr
και συμβολίζεται με pr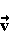
 .
.


Εάν |
| , | λ( |
|
| , |
Εάν |
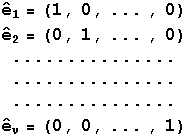
Τα διανύσματα αυτά είναι μοναδιαία και ανά δύο ορθογώνια μεταξύ τους.
Επίσης κάθε διάνυσμα
Γενικώτερα, αν
|
Εάν
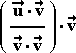 |
|
|