Τι είδους καμπύλες είναι οι ισοσταθμικές των παρακάτω συναρτήσεων;
i) f(x,y)=x2+y2 , ii) f(x,y)=y2-x2 , iii) f(x,y)=4-x-2y ,
iv) f(x,y)=xy , v) f(x,y)=x2/9 + y2/4 .
Γενικώς στην απάντηση για κάθε μια από τις παραπάνω συναρτήσεις δίνονται τρία σχήματα. Το πρώτο σχήμα είναι η αντιστοιχούσα επιφάνεια, το δεύτερο σχήμα οι ισοσταθμικές και στο τρίτο σχήμα είναι πάλι το δεύτερο σχήμα των ισοσταθμικών χρωματισμένο με αποχρώσεις του γκρί. Σκουρότερες περιοχές αντιστοιχούν σε οριζόντιες τομές (z=c) με μικρότερο c και λιγότερο σκούρες περιοχές σε οριζόντιες τομές (z=c) με μεγαλύτερο c.
Απαντήσεις:
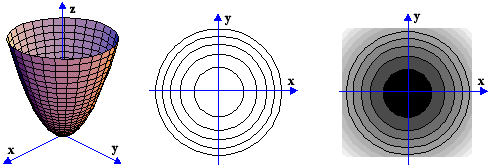
i) H f(x,y)=x2+y2 είναι κυκλικό παραβολοειδές (πρώτο σχήμα), και οι ισοσταθμικές του, δηλαδή οι οριζόντιες τομές του προβαλλόμενες στο xy-επίπεδο, είναι ομόκεντροι κύκλοι (δεύτερο σχήμα). Οι τομές της επιφανείας με επίπεδα παράλληλα προς τον z-άξονα είναι παραβολές που ανοίγουν προς την ίδια κατεύθυνση.
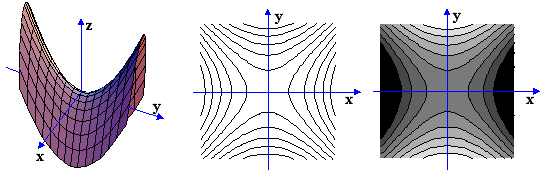
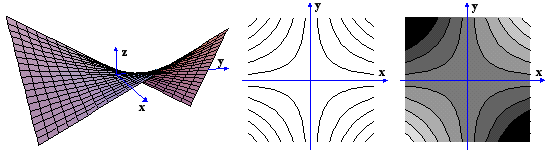
ii) Η f(x,y)=y2-x2 είναι υπερβολικό παραβολοειδές (πρώτο σχήμα), και οι ισοσταθμικές του είναι υπερβολές (δεύτερο σχήμα).Οι τομές της επιφανείας με επίπεδα παράλληλα προς τον z-άξονα είναι παραβολές που ανοίγουν και προς τις δύο κατευθύνσεις.
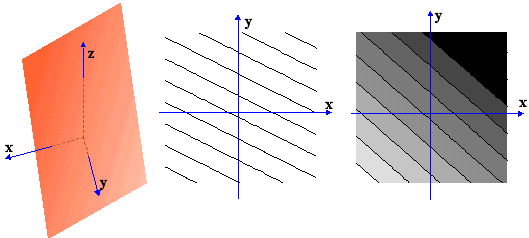
iii) Η f(x,y)=4-x-2y είναι ένα επίπεδο (πρώτο σχήμα), και οι ισοσταθμικές του είναι παράλληλες ευθείες (δεύτερο σχήμα).
iv) Η f(x,y)=xy είναι υπερβολικό παραβολοειδές (πρώτο σχήμα), και οι ισοσταθμικές του είναι υπερβολές (δεύτερο σχήμα).Οι τομές της επιφανείας με επίπεδα παράλληλα προς τον z-άξονα είναι παραβολές που ανοίγουν και προς τις δύο κατευθύνσεις.
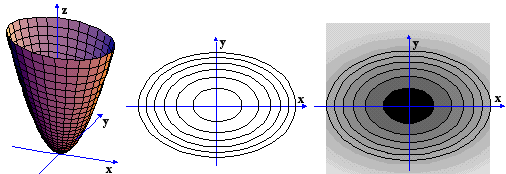
v) Η f(x,y)=x2/9 + y2/4 είναι ελλειπτικό παραβολοειδές (πρώτο σχήμα), και οι ισοσταθμικές του είναι ελλείψεις (δεύτερο σχήμα). Οι τομές της επιφανείας με επίπεδα παράλληλα προς τον z-άξονα είναι παραβολές που ανοίγουν προς την ίδια κατεύθυνση.