3.Ευθεία στο επίπεδο.Ημιεπίπεδα

3.1Εξισώσεις ευθείας
3.1.1Από σημείο και παράλληλο διάνυσμα
         Ευθεία που διέρχεται από το σημείο P(x_o,y_o) και είναι
         παράλληλη στο διάνυσμα
                              

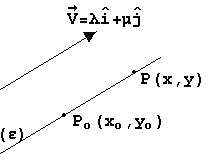
Διανυσματική εξίσωση

Παραμετρικές εξισώσεις     
x = x_o + λ t  ,  y = y_o+ μ t

Καρτεσιανή εξίσωση 
μ ( x - x_o ) - λ ( y - y_o) = 0




3.1.2Από σημείο και κάθετο σ'αυτήν διάνυσμα
       Ευθεία που διέρχεται από το σημείο P(x_o,y_o) και είναι
        κάθετη στο διάνυσμα
                     
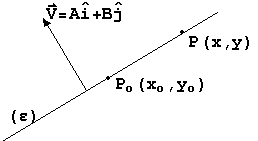Διανυσματική εξίσωση
       
  Καρτεσιανή εξίσωση
     Ax+By=C με C=Ax_o+By_o






3.1.3 Κλίση
Εστω ευθεία στο επίπεδο με εξίσωση Ax+By=C.
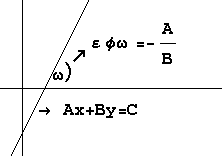
Το πηλίκον -A/B ονομάζεται κλίση της ευθείας και ισούται με την εφαπτομένη της γωνίας που σχηματίζει η ευθεία με τον x-άξονα.

 

3.2 Ημιεπίπεδα
Μια ευθεία Ax+By=C χωρίζει το επίπεδο σε δύο ημιεπίπεδα.
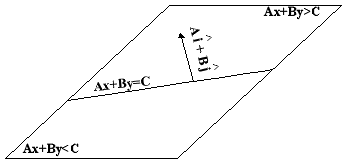
Όλα τα σημεία P(x,y) του ημιεπιπέδου που βρίσκονται προς την κατεύθυνση που "δείχνει" το διάνυσμα
        
αληθεύουν την ανισότητα Ax+By>C ενώ τα σημεία του άλλου ημιεπιπέδου την ανισότητα Ax+By<C

Ασκήσεις