
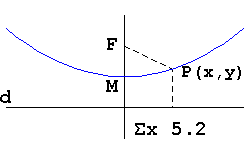
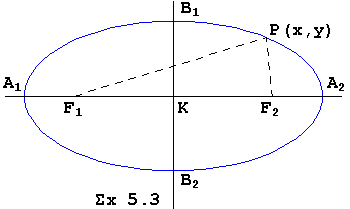
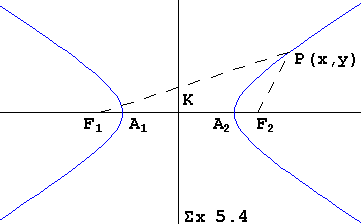
αx2+βxy+γy2+δx+εy=ζ (5.1) |
Πίνακας 5.1 |
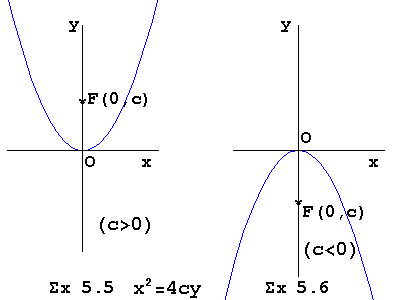
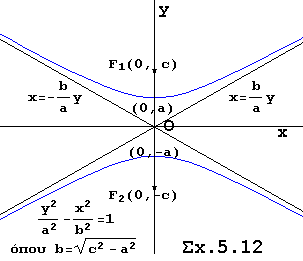
Πίνακας 5.2 |
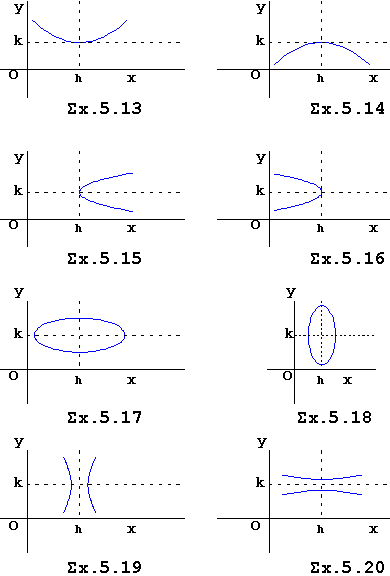
Παράλληλη μετατόπιση αξόνων ενός συστήματος καρτεσιανών συντεταγμένων |
Έστω σύστημα καρτεσιανών συντεταγμένων Oxy , το οποίο μετατοπίζεται στην θέση O'x'y' έτσι ώστε οι αντίστοιχοι άξονές του να είναι παράλληλοι και ομόρροποι.
|
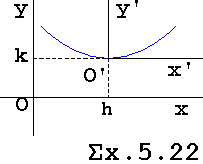
αx2+βxy+γy2+δx+εy=ζ όπου β=0 (5.3) |
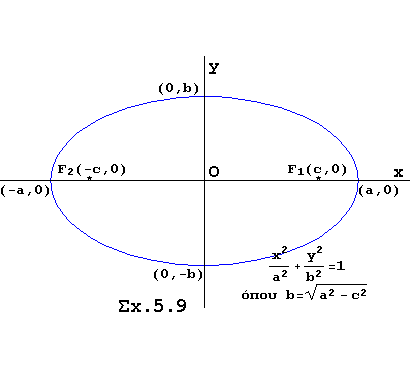
(1) Εάν αγ>0 τότε η (5.3) περιγράφει έλλειψη |
αx2+βxy+γy2+δx+εy=ζ
όπου β |
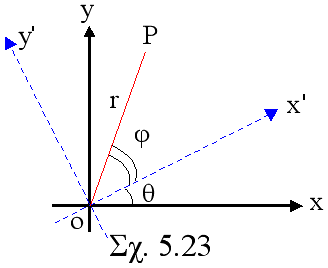
Περιστροφή αξόνων ενός
συστήματος καρτεσιανών συντεταγμένων
|
α'x'2+γ'y'2+δ'x'+ε'y'=ζ (5.6) |
Εάν |