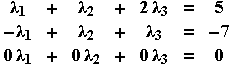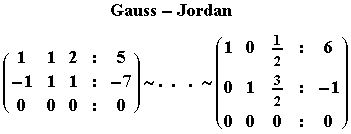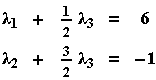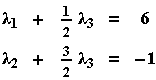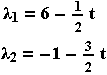Άσκηση:
Θεωρούμε τα διανύσματα ₁ = (1,-1,0) , ₂ = (1,1,0) , ₃ = (2,1,0) , = (5,-7,0).
(i) Να αποδειχθεί ότι L(₁ , ₂ , ₃)
(ii) Nα εκφρασθεί το ως γραμμικός συνδυασμός των ₁ , ₂ , ₃
Απάντηση
(i) Το L(₁ , ₂ , ₃) 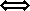υπάρχουν πραγματικοί αριθμοί λ₁ , λ₂ , λ₃ τέτοιοι ώστε =λ₁₁+λ₂₂+λ₃₃
( Εάν δηλαδή (5,-7,0)=λ₁(1,-1,0)+λ₂(1,1,0)+λ₃(2,1,0) )
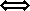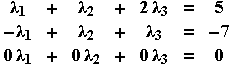
το παρακάτω γραμμικό σύστημα είναι συμβατό: ικανοποιούνται οι απαλοίφουσες εξισώσεις του.
Για να διερευνήσουμε αν ισχύει η προηγούμενη πρόταση , θεωρούμε τον επαυξημένο πίνακα του γραμμικού συστήματος και εφαρμόζουμε σ'αυτόν την διαδικασία των Gauss-Jordan. 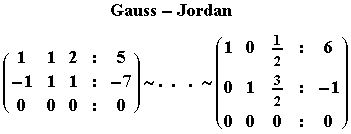Ο πίνακας Απλής Κλιμακωτής Μορφής που προκύπτει είναι ο επαυξημένος πίνακας του γραμμικού συστήματος

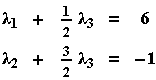0 = 0

που έχει τις ίδιες λύσεις με το αρχικό γραμμικό σύστημα. Η απαλοίφουσα εξίσωση του παραπάνω γραμμικού συστήματος ικανοποιείται , άρα αυτό είναι συμβατό , επομένως και το αρχικό σύστημα είναι συμβατό:
Άρα (5,-7,0) L((1,-1,0),(1,1,0),(2,1,0))
(ii) Για να εκφράσουμε το ως γραμμικό συνδυασμό των ₁ , ₂ , ₃ , αρκεί να βρούμε μια λύση του συστήματος

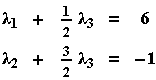0 = 0

το οποίο έχει άπειρο αριθμό λύσεων. Πράγματι εάν θέσουμε λ₃ = t ( όπου t ) , έχουμε 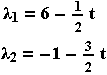Όταν t = -2 , λ₁ = 7 , λ₂ = 7 , λ₃ = -2 . Άρα έχουμε (5,-7,0) = 7(1,-1,0)+2(1,1,0)+(-2)(2,1,0)

---