Απαντήσεις στις Ασκήσεις 1ου Κεφαλαίου


1) Να λυθούν τα παρακάτω γραμμικά συστήματα, χρησιμοποιώντας τον αλγόριθμο των Gauss-Jordan.

(i)

(ii)

(iii)

x + 2y - 3z = -1
3x - y + z =  7
5x + 3y - 4z =  2

x + 2y + 2z =  2
3x - 2y - z =  5
2x - 5y + 3z = -4
x + 4y + 6z =  0

x + 5y + 4z - 13w = 3
3x - y + 2z + 5w = 2
2x + 2y + 3z - 4w = 1

(Σε κάθε περίπτωση να βρεθούν επίσης ο βαθμός του συστήματος , ο αριθμός ελεύθερων μεταβλητών και ο αριθμός βασικών μεταβλητών.)


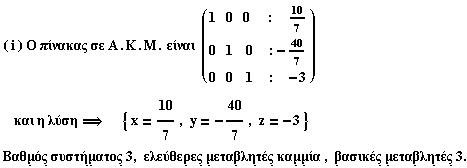
Σύστημα συμβατό
2) Nα βρεθούν συνθήκες για τα a , b , c ώστε να είναι συμβατά τα γραμμικά συστήματα:

(i)

(ii)

x + 2y - 3z = a
3x - y + z = b
-2x + 3y - 3z = c

x - 2y + z = a
x + y - z = b
2x - y - z = c

(i)

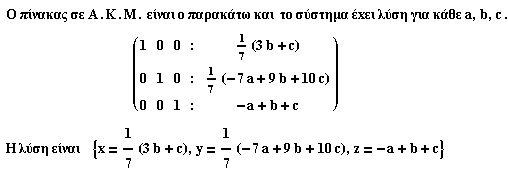
(ii)
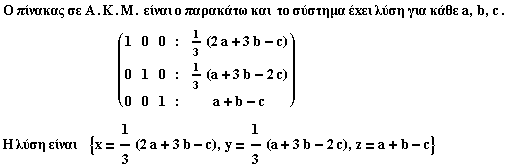
3) Να βρεθούν οι τιμές του k για τις οποίες τα παρακάτω γραμμικά συστήματα έχουν καμμία λύση , μια λύση , πολλές λύσεις :

(i)

(ii)

kx + y + z = 1
x + ky + z = 1
x + y + kz = 1

x + 2y + kz = 1
2x + ky + 8z = 3

i)

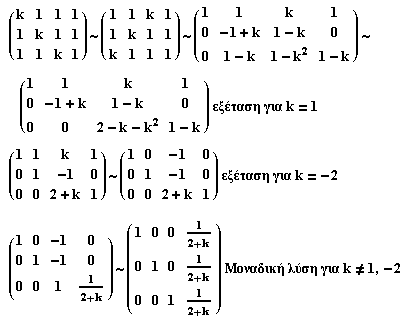
Όταν k=1 το σύστημα γίνεται η εξίσωση x+y+z = 1 και έχει άπειρες λύσεις με δύο, από τις τρεις μεταβλητές, ελεύθερες.
Όταν k = -2 το σύστημα δεν έχει καμμία λύση διότι άν προστεθούν οι τρεις εξισώσεις δίνουν 0 = 3.
Όταν το k είναι διάφορο από -2 ή 1 τότε το σύστημα έχει μια μόνο λύση που δίνεται από τις σχέσεις x = y = z = 1/(k+2)
ii)

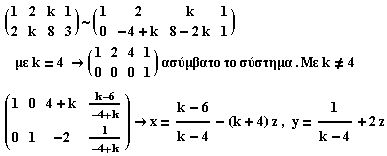
Όταν k = 4 το σύστημα γίνεται {x+2y+4z = 1 , 2x+4y+8z = 3} που είναι μη συμβατό.
Όταν k δεν είναι 4 τότε το σύστημα έχει άπειρες λύσεις με μια μεταβλητή ελεύθερη.
Οι λύσεις δίνονται από τις παρακάτω σχέσεις (όπου ελεύθερη μεταβλητή είναι η z ) ,
{ x = - (6-k-16z+k2z)/(k-4) , y = (1-8z+2kz)/(k-4) }.