Έστω D υποσύνολο του xy-επιπέδου. Κάθε κανόνας f, ο οποίος αντιστοιχεί ακριβώς έναν πραγματικό αριθμό f(x,y) σε κάθε στοιχείο (x,y) του D, ονομάζεται συνάρτηση δύο μεταβλητών με πεδίο ορισμού το D.
Παραδείγματα
α) f(x,y) = x2y+5
Πεδίο ορισμού της f, είναι όλο το xy-επίπεδο.
β) f(x,y) =
Πεδίο ορισμού της f, είναι το σύνολο των σημείων (x,y) για τα οποία ισχύει x2+y2 < 1. Δηλαδή είναι το σύνολο των σημείων ενός κλειστού δίσκου που έχει κέντρο στο (0,0) και ακτίνα 1.
Εάν z=f(x,y), οι μεταβλητές x και y ονομάζονται ανεξάρτητες μεταβλητές, ενώ η z εξαρτημένη μεταβλητή.
6.2: Γραφική παράσταση

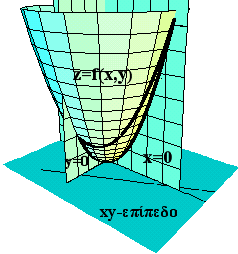
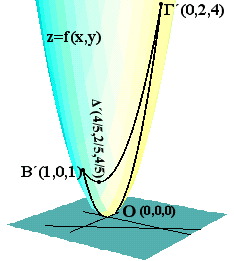
Γραφική παράσταση της f ονομάζουμε το σύνολο των σημείων (x,y,z) των οποίων οι συντεταγμένες ικανοποιούν την εξίσωση z=f(x,y). (Δηλαδή για να σχηματίσουμε την γραφική παράσταση της f παριστάνουμε τις τιμές της f(x,y) ως ύψη z πάνω από τα αντίστοιχα σημεία (x,y). Η γραφική παράσταση μιας συνάρτησης δύο μεταβλητών είναι μια επιφάνεια στον τρισδιάστατο χώρο.
Παραδείγματα
α) f(x,y) = x2+y2 β) f(x,y) =
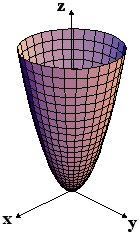
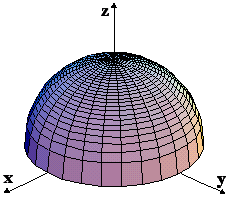
γ) f(x,y) = x2-y2 δ) f(x,y) =
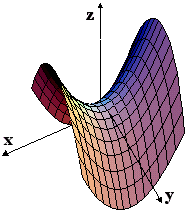
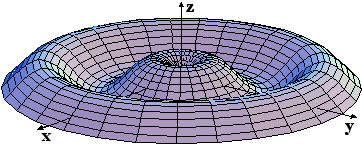
6.3: Ισοσταθμικές καμπύλες
Έστω συνάρτηση z=f(x,y). Θεωρούμε ένα επίπεδο Π, με εξίσωση z=c, το οποίο τέμνει την γραφική παράσταση της f. (Προφανώς το Π είναι παράλληλο προς το xy-επίπεδο και ο αριθμός |c| προσδιορίζει την απόσταση του Π απ'αυτό.)
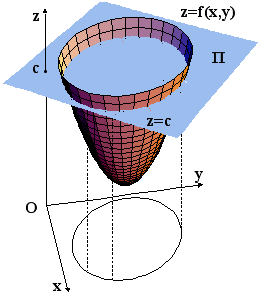
Η τομή του Π με την επιφάνεια z=f(x,y), θα είναι μια καμπύλη στο χώρο, η οποία έχει για σημεία της , όλα τα σημεία (x,y,z) για τα οποία ισχύει: z=f(x,y) και z=c. Δηλαδή θα είναι όλα τα σημεία (x,y,c) για τα οποία f(x,y)=c. Προβάλλουμε την καμπύλη αυτή πάνω στο xy-επίπεδο. Η προβολή της, θα είναι μια καμπύλη που θα έχει για σημεία της, όλα τα σημεία (x,y,0) για τα οποία ισχύει f(x,y)=c. Με άλλα λόγια θα είναι μια καμπύλη στο xy-επίπεδο στα σημεία της οποίας η f παίρνει σταθερή τιμή c. Καμπύλες αυτού του τύπου θα τις ονομάζουμε ισοσταθμικές καμπύλες της f.
Ερώτηση:
Τι είδους καμπύλες είναι οι ισοσταθμικές των παρακάτω συναρτήσεων;
i) f(x,y)=x2+y2 , ii) f(x,y)=y2-x2 , iii) f(x,y)=4-x-2y ,
iv) f(x,y)=xy , v) f(x,y)=x2/9 + y2/4 . Απαντήσεις ( i , ii , iii , iv , v )
Παρατήρηση: Όπως είδαμε και προηγουμένως, οι ισοσταθμικές καμπύλες μιας συνάρτησης αποτελούν ουσιαστικά την αποτύπωση της γραφικής της παράστασης στο xy-επίπεδο. Επομένως αυτές μπορούν να μας φανούν χρήσιμες στο να βγάζουμε συμπεράσματα για την μορφή που θα έχει η γραφική παράσταση μιας συνάρτησης δύο μεταβλητών.
6.4: Συνέχεια
Μια ακολουθία σημείων < Pi ( xi , yi ) > θα λέμε ότι τείνει σε κάποιο σημείο Po(xo , yo ) αν το ίδιο ισχύει για τις ακολουθίες των αντιστοίχων συντεταγμένων τους. δηλαδή Pi ( xi , yi )
Μια συνάρτηση f(x,y) θα λέμε ότι είναι συνεχής σε κάποιο σημείο Po αν για κάθε ακολουθία σημείων Pi που τείνει σ'αυτό (Pi
Οι ασυνέχειες μιας συνάρτησης δύο μεταβλητών εκδηλώνονται γεωμετρικά με "διακοπές" της επιφανείας που αποτελεί την γραφική της παράσταση.
Παράδειγμα Θεωρούμε την συνάρτηση
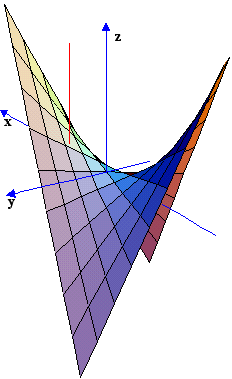 Εδώ υπάρχουν
ακολουθίες σημείων Pi , οι οποίες τείνουν
στο σημείο (2,3) και για τις οποίες έχουμε f(Pi)
Εδώ υπάρχουν
ακολουθίες σημείων Pi , οι οποίες τείνουν
στο σημείο (2,3) και για τις οποίες έχουμε f(Pi)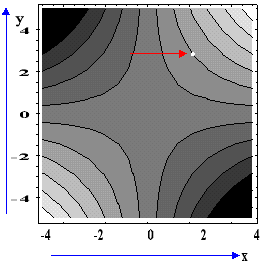
Την ασυνέχεια της f(x,y) μπορούμε να διακρίνουμε από την γραφική παράσταση των ισοσταθμικών της. Το οριζόντιο επίπεδο z=24 τέμνει την επιφάνεια έτσι ώστε η αντίστοιχη ισοσταθμική παρουσιάζει ασυνέχεια στο σημείο (2,3).
Η συνάρτηση θα γίνει συνεχής εάν ορίσουμε να παίρνει την τιμή 24 όταν (x,y)=(2,3). Δηλαδή να είναι f(2,3)=24.
6.5:Περιοχές του επιπέδου
Μια εξίσωση της μορφής g(x,y)=c ορίζει μια καμπύλη στο xy-επίπεδο, η οποία το χωρίζει σε δύο υποπεριοχές, όπου τα σημεία της καθεμιάς ικανοποιούν μια από τις ανισώσεις.
g(x,y) < c ή g(x,y) > c (6.1)
Παράδειγμα
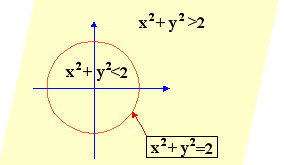 Η ανισότητα x2+y2>2
χαρακτηρίζει τα εκτός της περιφέρειας σημεία του
επιπέδου ενώ η x2+y2<2 χαρακτηρίζει τα
εσωτερικά σημεία της περιφέρειας.
Η ανισότητα x2+y2>2
χαρακτηρίζει τα εκτός της περιφέρειας σημεία του
επιπέδου ενώ η x2+y2<2 χαρακτηρίζει τα
εσωτερικά σημεία της περιφέρειας.
Έχουμε επίσης τις σχέσεις
g(x,y) <
c ή g(x,y) > c
(6.2)
Όπου η καθεμιά μαζί με την αντίστοιχη περιοχή
περιλαμβάνει και τα σημεία της καμπύλης
g(x,y) = c
(6.3)
Υποθέτοντας ότι η συνάρτηση g είναι συνεχής
ονομάζουμε τις περιοχές της μορφής (6.1) ανοικτές
και αυτές της μορφής (6.2) κλειστές. Σε όλες αυτές
τις περιπτώσεις η καμπύλη (6.3) ονομάζεται σύνορο
της περιοχής.Έτσι μια κλειστή περιοχή περιέχει
και το σύνορό της ενώ μια ανοικτή δεν το περιέχει.
Μια περιοχή ονομάζεται φραγμένη αν
περιέχεται μέσα σε κάποιο κύκλο δηλαδή αν τα
σημεία της δεν τείνουν στο άπειρο.
Μια κλειστή και φραγμένη περιοχή ονομάζεται
συμπαγής.
Γειτονιά ενός σημείου (xo,yo) στο
επίπεδο θα ονομάζουμε έναν ανοικτό δίσκο Ν, ο
οποίος έχει για κέντρο του το (xo,yo). Με
άλλα λόγια
![]()
όπου ο r εκφράζει την ακτίνα του δίσκου Ν.
6.6: Μερικές παράγωγοι
Έστω συνάρτηση z=f(x,y), την οποία
θεωρούμε σε κάποιο σημείο (x,y) του πεδίου ορισμού
της. Κρατάμε την μεταβλητή y σταθερή και
μεταβάλλουμε την x κατά Δx. Η μεταβολή στην τιμή
της f θα είναι:
Δxz=Δxf=f(x+Δx,y)-f(x,y) και
επομένως το όριο
![]() (6.4)
(6.4)
θα εκφράζει τον οριακό ρυθμό μεταβολής στις
τιμές της f, ως προς την μεταβολή της x.
Στην συνέχεια κάνουμε το ίδιο, κρατώντας
αυτή την φορά την μεταβλητή x σταθερή και
μεταβάλλοντας την y κατά Δy. Η μεταβολή στην τιμή f
θα είναι: Δyz=Δyf=f(x,y+Δy)-f(x,y) και
επομένως το όριο
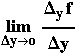 (6.5)
(6.5)
θα εκφράζει τον οριακό ρυθμό μεταβολής στις
τιμές της f, ως προς την μεταβολή της y.
Τα όρια των (6.4) και (6.5) τα ονομάζουμε μερικές
παράγωγοι της f ως προς x και y αντίστοιχα και τις
συμβολίζουμε με fx(x,y) και fy(x,y) ή
![]()
Δηλαδή έχουμε
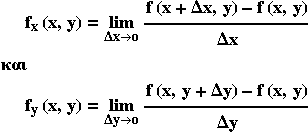
Παράδειγμα: Θεωρούμε την
συνάρτηση f(x,y)=x2-xy+y2
Έχουμε
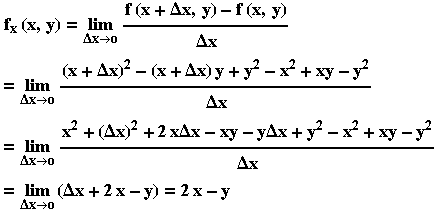
και
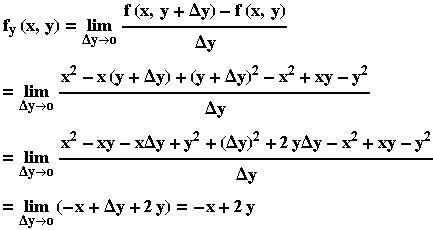
Παρατήρηση: Επειδή στον ορισμό των μερικών
παραγώγων κρατάμε πάντα την μια μεταβλητή
σταθερά, αυτές μπορούν να θεωρηθούν σαν οι
συνηθισμένες παράγωγοι ως προς την άλλη
μεταβλητή.
Έτσι στην πράξη μπορούμε να
αποφύγουμε την διαδικασία των ορίων και να
παραγωγίζουμε χρησιμοποιώντας όλους τους
γνωστούς κανόνες παραγώγισης που γνωρίζουμε για
τις συναρτήσεις με μια μεταβλητή.
Παράδειγμα: Εάν f(x,y)=x2+xy3+exy,
έχουμε
fx(x,y)=2x+y3+exyy , fy(x,y)=3y2x+exyx.
6.7: Γεωμετρική ερμηνεία
μερικών παραγώγων
Έστω συνάρτηση f με τύπο
z=f(x,y). Θεωρούμε την μερική παράγωγο της f ως προς x,
σε κάποιο σημείο (xo,yo) του πεδίου
ορισμού της. Θα έχουμε
![]() (6.6)
(6.6)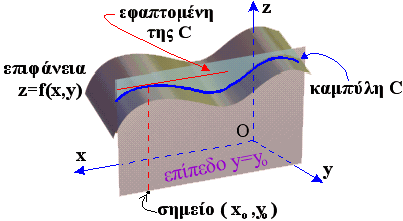
Η τομή της επιφανείας, που αποτελεί την
γραφική παράσταση της f(x,y), και του
επιπέδου y=yo, θα είναι μια καμπύλη C στον
τρισδιάστατο χώρο. Η καμπύλη C θα περιέχει για
σημεία της, όλα τα σημεία (x,y,z) για τα οποία ισχύει:
z=f(x,y) και y=yo , δηλαδή η C θα έχει για σημεία
της , όλα τα σημεία (x,yo,z) για τα οποία ισχύει
z=f(x,yο). Η σχέση z=f(x,yο) ορίζει μια
συνάρτηση μιας μεταβλητής, η γραφική παράσταση
της οποίας είναι πάνω στο xz-επίπεδο. Άρα η γραφική
παράσταση της z=f(x,yο) θα αποτελεί ουσιαστικά
την προβολή της C πάνω στο xz-επίπεδο.
Ορίζουμε g(x)=f(x,yo) και παρατηρούμε ότι g΄(x)=fx(x,yo).
Άρα g΄(xο)=fx(xο,yo) ( Βλέπε σχέση
6.6 ) και επομένως ο αριθμός fx(xο,yo)
εκφράζει την κλίση της εφαπτόμενης ευθείας στην
καμπύλη C στο σημείο P(xo , yo , f(xo,yo)).
Σημείωση: Η γεωμετρική ερμηνεία της
άλλης μερικής παραγώγου είναι αντίστοιχη.
6.8: Δεύτερες μερικοί παράγωγοι
Οι μερικές παράγωγοι fx(x,y)
και fy(x,y) μιας συνάρτησης f(x,y) δύο μεταβλητών
είναι επίσης συναρτήσεις δύο μεταβλητών και
μπορούν να παραγωγιστούν εκ νέου δίνοντας τις
δεύτερες μερικές παραγώγους που είναι τέσσερεις
τον αριθμό: fxx(x,y) , fxy(x,y) , fyx(x,y) , fyy(x,y)
ή
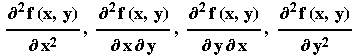 αντίστοιχα.
αντίστοιχα.
Παράδειγμα: Θεωρούμε την συνάρτηση f(x,y)=x3y-xy2
οπότε έχουμε,
fx(x,y)=3x2y-y2
fy(x,y)=x3-2yx
fxy(x,y)=3x2-2y
fyx(x,y)=3x2-2y
fxx(x,y)=6xy
fyy(x,y)=-2x
6.9: Αλυσωτή παραγώγιση
Οι μεταβλητές που εμφανίζονται σ'ένα πρόβλημα
μπορεί να συνδέονται μεταξύ τους με περισσότερες
από μια συναρτήσεις.
Για παράδειγμα μπορεί να έχουμε μια εξαρτημένη
μεταβλητή z που δίνεται από την συνάρτηση z=f(x,y),
όπου τα x,y δεν είναι ανεξάρτητα , αλλά
καθορίζονται από τις τιμές άλλων μεταβλητών s,t
μέσω συναρτήσεων x=x(s,t), y=y(s,t). οι οποίες
επίσης μπορεί να καθορίζονται ως συναρτήσεις
άλλων μεταβλητών κ.ο.κ.
Μια τέτοια σύνθεση συναρτήσεων περιγράφεται από
ένα γράφημα που ονομάζεται ΔΕΝΤΡΟ ΕΞΑΡΤΗΣΗΣ ΤΩΝ
ΜΕΤΑΒΛΗΤΩΝ.
Παραδείγματα:
α) Έστω z=f(x,y) όπου x=x(s,t) και y=y(s,t).
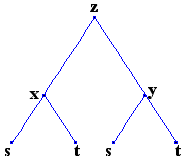
Δέντρο εξάρτησης μεταβλητών
z : εξαρτημένη μεταβλητή
x,y : ενδιάμεσες μεταβλητές
s,t : ανεξάρτητες μεταβλητές
β)Έστω z=f(x,y) όπου x=x(t) και y=y(t).
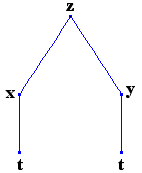
Δέντρο εξάρτησης μεταβλητών
z : εξαρτημένη μεταβλητή
x,y : ενδιάμεσες μεταβλητές
t : ανεξάρτητη μεταβλητή
Στους
διάφορους τύπους αλυσωτής παραγώγισης
εκφράζουμε
|
Ο πρώτος κανόνας
αλυσωτής παραγώγισης που θα αναφέρουμε έχει
σχέση με την περίπτωση του παραδείγματος β.
Έστω z=f(x,y), όπου x=x(t)
και y=y(t).Τότε η z μπορεί να εκφρασθεί σαν
συνάρτηση του t, z=f(x(t),y(t))=f(t) και η
παράγωγός της είναι:
|
Ας επαληθεύσουμε τον
προηγούμενο κανόνα για το εξής παράδειγμα :
z=f(x,y)=x2+xy, όπου x=x(t)=2t και y=y(t)=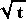 .
.
Τότε έχουμε z=f(t)=4t2+2t3/2
Για τις παραγώγους των παραπάνω συναρτήσεων
ισχύουν τα εξής:
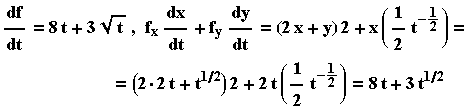
Δηλαδή επαληθεύεται ο προηγούμενος κανόνας.
Γενικά για να
προσδιορίσουμε έναν τύπο αλυσωτής
|
1) Κατασκευάζουμε το δέντρο εξάρτησης των μεταβλητών. |
2) Σε κάθε
ακμή του, αντιστοιχούμε την παράγωγο της
|
3) Βρίσκουμε
τα "μονοπάτια" που συνδέουν την εξαρτημένη
|
4) Σε κάθε
μονοπάτι του βήματος 3, αντιστοιχούμε
|
5) Το
άθροισμα των γινομένων του βήματος 4,
|
Ας δούμε αυτή τη διαδικασία, να εφαρμόζεται σε
κάποια παραδείγματα.
Παραδείγματα:
α) Έστω z=z(x,y), όπου y=y(x). Σ'αυτή την περίπτωση η z
μπορεί να εκφρασθεί σαν συνάρτηση του x,
z=z(x,y(x))=z(x)
και η παράγωγος θα είναι:
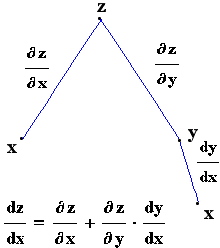
β) Έστω z=z(x,y) όπου x=x(s,t) και y=y(s,t). Εδώ η z μπορεί
να εκφρασθεί σαν συνάρτηση των s , t 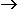 z=z(x(s,t),y(s,t))=z(s,t) και οι μερικές
παράγωγοι θα είναι:
z=z(x(s,t),y(s,t))=z(s,t) και οι μερικές
παράγωγοι θα είναι:
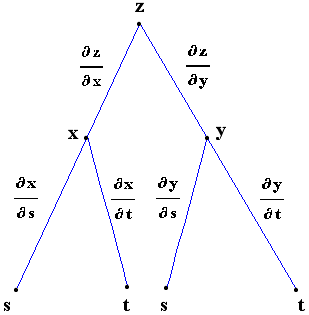
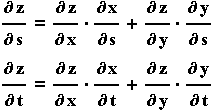
γ) Έστω z=z(x,y) όπου y=y(x,t). Εδώ η z μπορεί να εκφρασθεί
σαν συνάρτηση των x , t 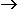 z=z(x,y(x,t))=z(x,t)
και οι μερικές παράγωγοι θα είναι:
z=z(x,y(x,t))=z(x,t)
και οι μερικές παράγωγοι θα είναι:
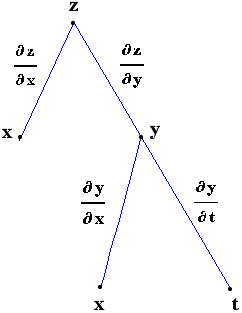
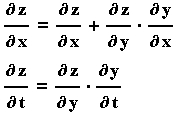
(6.7)
Παρατήρηση: Εδώ παρατηρούμε ότι τα 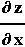 που
εμφανίζονται στο αριστερό και το δεξιό μέλος της
(6.7) είναι εντελώς διαφορετικά μεγέθη.
που
εμφανίζονται στο αριστερό και το δεξιό μέλος της
(6.7) είναι εντελώς διαφορετικά μεγέθη.
Στο αριστερό μέλος έχουμε την τελική εξάρτηση
του z από τα x και t, ενώ στο δεξιό μέλος, την
ενδιάμεση εξάρτηση του z από τα x και y. Δηλαδή
έχουμε :
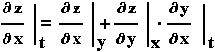
όπου οι δείκτες δηλώνουν τις μεταβλητές που
κρατάμε σταθερές στην διαδικασία της
παραγώγισης.
Ας επαληθεύσουμε τον προηγούμενο κανόνα
αλυσωτής παραγώγισης, για ένα συγκεκριμένο
παράδειγμα.
Έστω z=z(x,y)=xy όπου y=y(x,t)=x+xt.
Τότε έχουμε z=z(x,y(x,t))=z(x.t)=x(x+xt)=x2+x2t.
Για τις παραγώγους των παραπάνω συναρτήσεων
ισχύουν τα εξής :
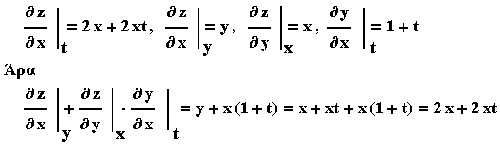
και επομένως επαληθεύεται ο κανόνας (6.7).
6.10: Παράγωγος κατά κατεύθυνση
Στο Κεφ 6.6 ορίσαμε για
μια συνάρτηση f δύο μεταβλητών τις μερικές
παραγώγους, οι οποίες εκφράζουν τους οριακούς
ρυθμούς μεταβολής στις τιμές της, για
μετατοπίσεις στο xy-επίπεδο κατά την κατεύθυνση
των δύο αξόνων.
Υπενθυμίζουμε
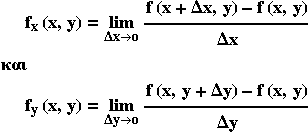
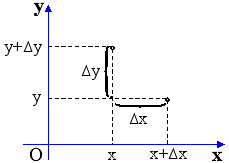
Μπορούμε τώρα να
θεωρήσουμε μετατοπίσεις Δs στο xy-επίπεδο προς
κατευθύνσεις διαφορετικές από αυτές των δύο
αξόνων. Μια τέτοια κατεύθυνση καθορίζεται από
την γωνία θ που σχηματίζει με τον x-άξονα και
αντιστοιχεί σε ταυτόχρονη μεταβολή των x και y
κατά:
Δx=Δs cosθ και Δy=Δs sinθ
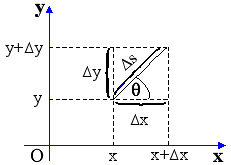
Ορισμός Η παράγωγος της f κατά κατεύθυνση θ,
στο σημείο (x,y) συμβολίζεται με Dθf(x,y) και
ορίζεται ως το μέγεθος
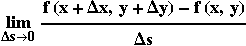
Όπως βλέπουμε στον
προηγούμενο ορισμό η Dθf(x,y) εκφράζει τον
οριακό ρυθμό μεταβολής στις τιμές της f για
μετατοπίσεις στο xy-επίπεδο κατά την κατεύθυνση
που σχηματίζει γωνία θ με τον x-άξονα.
Το επόμενο θεώρημα που
θα αναφέρουμε, είναι πολύ χρήσιμο στον
υπολογισμό του ορίου με το οποίο ισούται η Dθf(x,y).
Θεώρημα 6.1:
Έστω z=f(x,y) συνεχής συνάρτηση της οποίας οι
μερικές παράγωγοι fx(x,y) και fy(x,y) είναι
επίσης συνεχείς. Έστω επίσης ότι μεταβολές Δx και
Δy ως προς τις μεταβλητές x και y επιφέρουν
μεταβολή Δz ως προς την μεταβλητή z.
|
Χρησιμοποιώντας το
θεώρημα 6.1 έχουμε τα εξής:
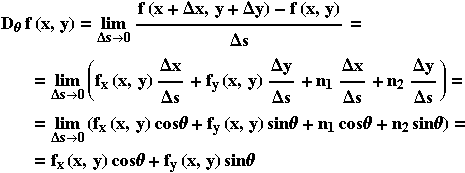
διότι όταν Δs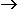 0 , Δx , Δy
0 , Δx , Δy 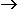 0 και άρα n1 , n2
0 και άρα n1 , n2
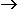 0
0
Επομένως
Dθf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ |
Παρατηρήσεις:
(1) D0f(x,y)=fx(x,y) , Dπ/2f(x,y)=fy(x,y)
(2) Εάν ονομάσουμε το διάνυσμα 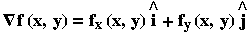 , διάνυσμα
κλίσης της f στο (x,y), παρατηρούμε ότι:
, διάνυσμα
κλίσης της f στο (x,y), παρατηρούμε ότι:
Dθf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ=(fx(x,y)
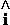 +fy(x,y)
+fy(x,y)
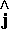 ).(cosθ
).(cosθ 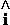 +sinθ
+sinθ 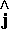 )=
)=
(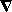 f(x,y))(cosθ
f(x,y))(cosθ 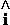 +sinθ
+sinθ 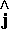 ) όπου (cosθ
) όπου (cosθ 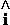 +sinθ
+sinθ 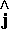 ) το μοναδιαίο διάνυσμα στην
κατεύθυνση θ.
) το μοναδιαίο διάνυσμα στην
κατεύθυνση θ.
Όμως (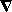 f(x,y))(cosθ
f(x,y))(cosθ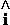 +sinθ
+sinθ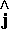 ) =|
) =|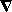 f(x,y)|cosφ
όπου φ η γωνία που σχηματίζει το
f(x,y)|cosφ
όπου φ η γωνία που σχηματίζει το 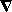 f(x,y)
με την κατεύθυνση θ.
f(x,y)
με την κατεύθυνση θ.
Άρα Dθf(x,y)=|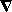 f(x,y)|cosφ και επομένως
-|
f(x,y)|cosφ και επομένως
-|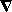 f(x,y)| < Dθf(x,y)
< |
f(x,y)| < Dθf(x,y)
< |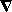 f(x,y)|.
f(x,y)|.
Εάν φ=0 Dθf(x,y)=|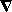 f(x,y)|
f(x,y)|
Εάν φ=π Dθf(x,y)=-|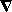 f(x,y)|
f(x,y)|
όλα αυτά μας επιτρέπουν να βγάλουμε τα εξής
συμπεράσματα.
- H f αυξάνεται περισσότερο προς την κατεύθυνση
του
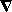 f.
f. - H f μειώνεται περισσότερο προς την αντίθετη
κατεύθυνση του
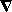 f.
f. - Ο ρυθμός μεταβολής είναι μηδενικός όταν φ=π/2 ή φ=3π/2.
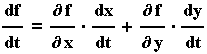

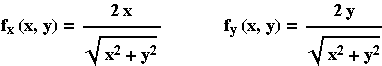
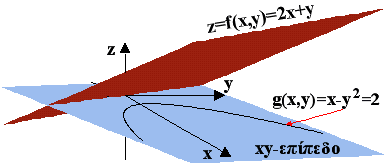
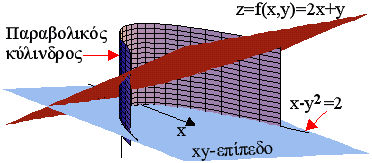 Τα σημεία (x,y) που
επαληθεύουν την x-y2=2 προσδιορίζουν επί του
επιπέδου z=2x+y μια καμπύλη C, που προκύπτει από την
τομή του επιπέδου z=2x+y και του παραβολικού
κυλίνδρου που δημιουργείται εάν φέρουμε
κατακόρυφες ευθείες κατά μήκος της παραβολής x-y2=2.
Τα σημεία (x,y) που
επαληθεύουν την x-y2=2 προσδιορίζουν επί του
επιπέδου z=2x+y μια καμπύλη C, που προκύπτει από την
τομή του επιπέδου z=2x+y και του παραβολικού
κυλίνδρου που δημιουργείται εάν φέρουμε
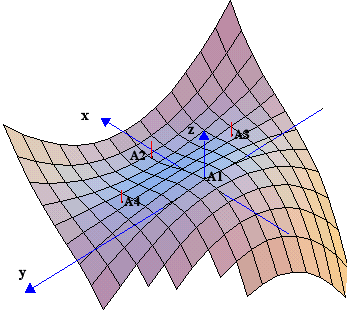
κατακόρυφες ευθείες κατά μήκος της παραβολής x-y2=2.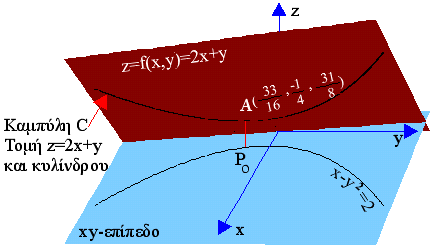 Στο διπλανό σχήμα
έχουμε το xy-επίπεδο, το z=2x+y επίπεδο, την παραβολή
x-y2=2, και την καμπύλη C επί του z=2x+y. Το σημείο Ρο
είναι το (
Στο διπλανό σχήμα
έχουμε το xy-επίπεδο, το z=2x+y επίπεδο, την παραβολή
x-y2=2, και την καμπύλη C επί του z=2x+y. Το σημείο Ρο
είναι το ( 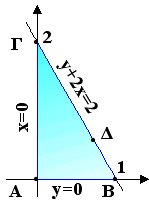
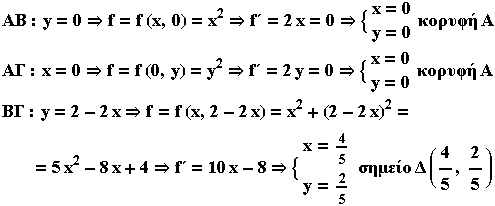
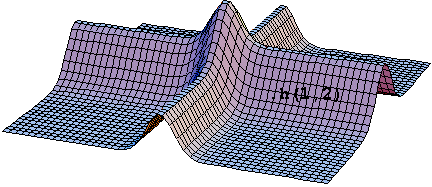
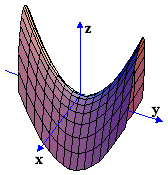
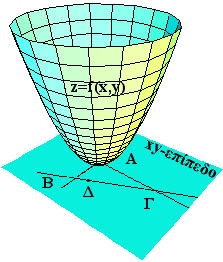 Στο διπλανό
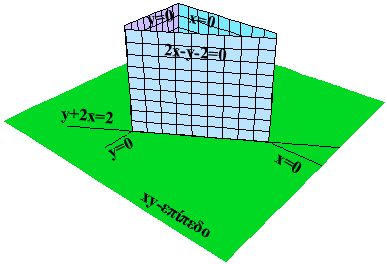
σχήμα είναι η γραφική παράσταση της z=f(x,y) = x2+y2,το
xy-επίπεδο και η τριγωνική περιοχή εντός της
οποίας τα x,y λαμβάνουν τιμές. Για να βρούμε το
τμήμα της επιφάνειας z=f(x,y) = x2+y2 που
μας ενδιαφέρει θα πρέπει να φέρουμε τρία
κατακόρυφα επίπεδα, με ίχνη στο xy-επίπεδο την
τριγωνική περιοχή, και το τμήμα που αποκόπτουν
από την z=f(x,y) = x2+y2 είναι το προς
εξέταση για τα ολικά ακρότατα.
Στο διπλανό
σχήμα είναι η γραφική παράσταση της z=f(x,y) = x2+y2,το
xy-επίπεδο και η τριγωνική περιοχή εντός της
οποίας τα x,y λαμβάνουν τιμές. Για να βρούμε το
τμήμα της επιφάνειας z=f(x,y) = x2+y2 που
μας ενδιαφέρει θα πρέπει να φέρουμε τρία
κατακόρυφα επίπεδα, με ίχνη στο xy-επίπεδο την
τριγωνική περιοχή, και το τμήμα που αποκόπτουν
από την z=f(x,y) = x2+y2 είναι το προς
εξέταση για τα ολικά ακρότατα.