Απαντήσεις ασκήσεων 6ου Κεφαλαίου

1. Δίνονται οι παρακάτω συναρτήσεις και οι ισοσταθμικές τους σε διαφορετική διάταξη. Να βρείτε την σωστή αντιστοίχιση : Ισοσταθμικές 

a) f(x,y)=e-x+y2          b) f(x,y)=ln(x2+y2)       c) f(x,y)=x2-xy         
d) f(x,y)=y/x               e) f(x,y)=4x2+y2-x+y.

Απάντηση :
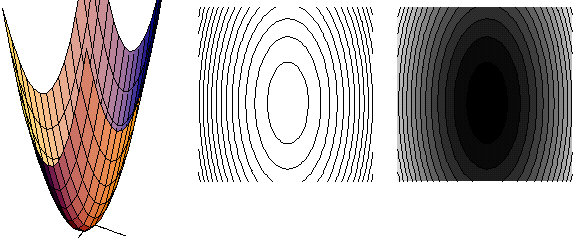
Γενικώς για κάθε μια από τις παραπάνω συναρτήσεις δίνονται τρία σχήματα. Το πρώτο σχήμα είναι η αντίστοιχη επιφάνεια, το δεύτερο σχήμα οι ισοσταθμικές και το τρίτο σχήμα είναι οι ισοσταθμικές, χρωματισμένες σε αποχρώσεις του γκρί. Σκουρότερες  περιοχές αντιστοιχούν σε οριζόντιες τομές (z=c) με μικρότερο c και λιγότερο σκούρες περιοχές σε  οριζόντιες τομές (z=c) με μεγαλύτερο c.
a) Οι ισοσταθμικές της f(x,y)=e-x+y2 είναι παραβολές της μορφής x=y2+c.

b) Οι ισοσταθμικές της f(x,y)=ln(x2+y2) κύκλοι της μορφής x2+y2=c.

c) Οι ισοσταθμικές της f(x,y)=x2-xy είναι υπερβολές της μορφής x2-xy=c. Περιστροφή αξόνων

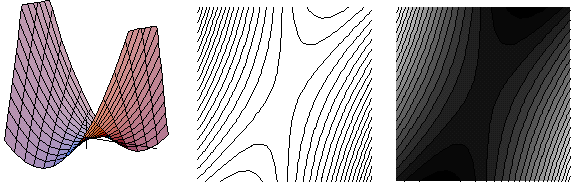
d) Οι ισοσταθμικές της f(x,y)=y/x είναι ευθείες της μορφής y/x=c. Δεν διέρχονται από την αρχή των αξόνων, διότι σημεία της μορφής (0,y) δεν ανήκουν στο πεδίο ορισμού της f(x,y).

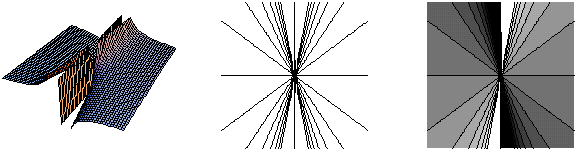
e) Οι ισοσταθμικές της f(x,y)=4x2+y2-x+y είναι ελλείψεις της μορφής 4x2+y2-x+y=c.
2. Να βρεθούν οι καμπύλες που προκύπτουν από την τομή των παρακάτω επιφανειών με τα επίπεδα συντεταγμένων :
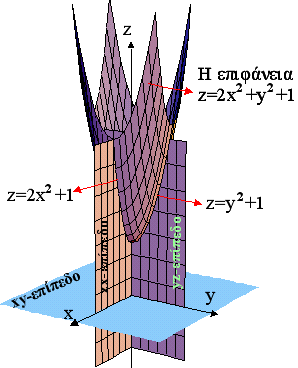
a) z=2x2+y2+1      b) z=x2-y      c) z+x+y2=1.
Απάντηση:
Σε όλες τις περιπτώσεις οι ζητούμενες καμπύλες που προκύπτουν (εάν το αντίστοιχο επίπεδο τέμνει την επιφάνεια) βρίσκονται επάνω στο επίπεδο που τέμνει την επιφάνεια. Οι τομές βρίσκονται εάν θέσουμε z=0 για το xy-επίπεδο , x=0 για το yz-επίπεδο και y=0 για το zx-επίπεδο.
a) Το xy-επίπεδο δεν τέμνει την επιφάνεια διότι για z=0 έχουμε 2x2+y2+1=0. Το x=0 δίνει την παραβολή z=y2+1. Το y=0 δίνει την παραβολή z=2x2+1.

b) Για z=0 έχουμε την παραβολή x2-y=0. Για x=0 έχουμε την ευθεία z=-y. Για y=0 έχουμε την παραβολή z=x2.

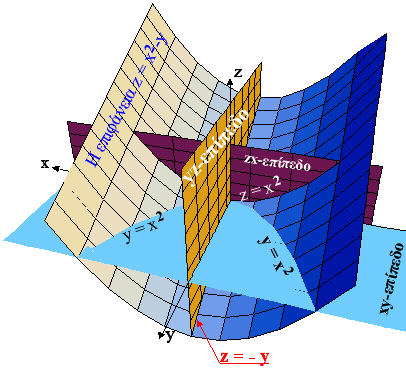
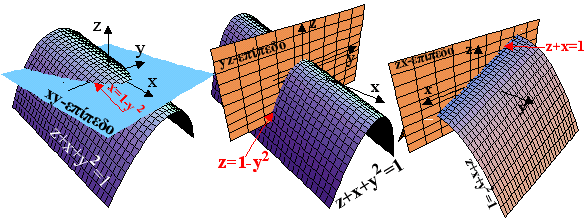
c) Για z=0 έχουμε την παραβολή x=1-y2 στο xy-επίπεδο. Για x=0 έχουμε την παραβολή z=1-y2 στο yz-επίπεδο. Για y=0 έχουμε την ευθεία z=1-x στο zx-επίπεδο.
3. Να δοθεί το δένδρο εξάρτησης και να επαληθευθούν οι κανόνες αλυσωτής παραγώγισης στις παρακάτω περιπτώσεις : Δένδρο εξάρτησης 

a) w=xy , x=t , y=sint            b) w=xy , x=s+t , y=s-t
c) z=x+y2 , y=lnx                   d) z=x2 , x=s+4t

Απάντηση:
Σύμφωνα με την διαδικασία για τον προσδιορισμό ενός τύπου αλυσωτής παραγώγισης και με την βοήθεια των δένδρων εξάρτησης έχουμε :
a) w=xy , x=t , y=sint

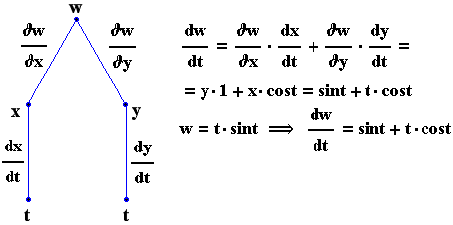
b) w=xy , x=s+t , y=s-t

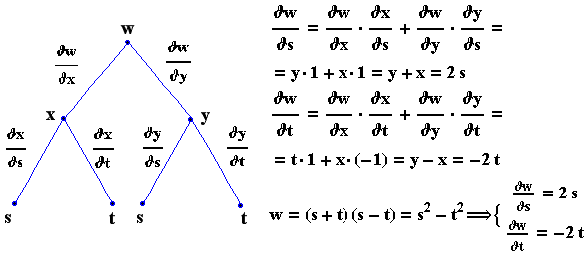
c) z=x+y2 , y=lnx

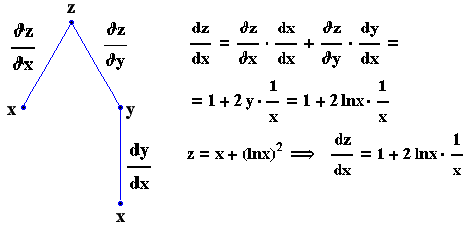
d) z=x2 , x=s+4t

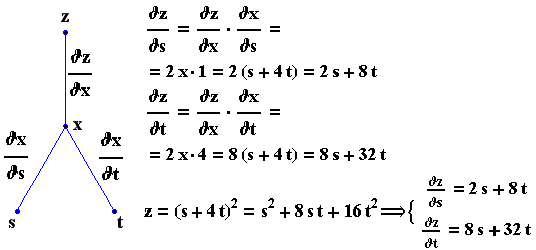
4. Για την συνάρτηση f(x,y)=4x2y να βρεθούν στο σημείο (-1 , 1) οι κατευθύνσεις προς τις οποίες η τιμή της f(x,y) :
α) Αυξάνει με το γρηγορώτερο ρυθμό
β) Ελαττώνεται με το γρηγορώτερο ρυθμό
γ) Παραμένει αμετάβλητη.Παράγωγος κατά κατεύθυνση Διάνυσμα κλίσης
Απάντηση:
α) Η συνάρτηση αυξάνει με το γρηγορώτερο ρυθμό προς την κατεύθυνση του διανύσματος f. Εδώ είναι f=8xy+4x2 και στο σημείο (-1,1) είναι f=-8+4. Η κατεύθυνση του f είναι (-2+)/.
β) Η ελάττωση με τον γρηγορώτερο ρυθμό είναι προς την αντίθετη κατεύθυνση δηλαδή προς την (2-)/.
γ) Η κατεύθυνση που η συνάρτηση παραμένει αμετάβλητη είναι η κάθετη προς την κατεύθυνση του f δηλαδή η (+2)/ και η (--2)/.



5. Η παράγωγος της f(x,y) στο σημείο Α(2,4) στην κατεύθυνση του διανύσματος + είναι και προς την κατεύθυνση του διανύσματος -3 είναι 4. Ποιά είναι η παράγωγος της f στην κατεύθυνση του διανύσματος 3-4; Παράγωγος κατά κατεύθυνση Διάνυσμα κλίσης
Απάντηση:





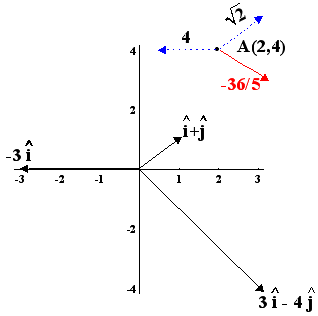
Είναι
(fx(2,4)+fy(2,4))(+)/=
και (fx(2,4)+fy(2,4))(-)=4.
Η λύση του συστήματος δίνει fx=-4 και fy=6 , οπότε έχουμε
(-4+6)(3-4)/5=-36/5.



6. Να βρεθούν και να χαρακτηρισθούν τα τοπικά ακρότατα σημεία της f(x,y)=x4+y4-8xy. Τοπικά ακρότατα
Απάντηση:
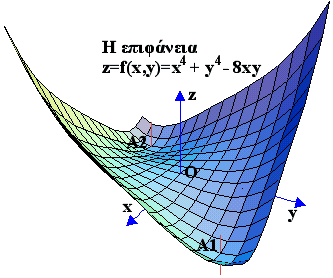Η συνάρτηση ορίζεται σε ολόκληρο το xy-επίπεδο. Οι πρώτες μερικές παράγωγοι είναι fx(x,y)=4x3-8y και fy(x,y)=4y3-8x. Η επίλυση του συστήματος 4x3-8y =0,4y3-8x=0 μας δίνει τρία ελεύθερα στάσιμα σημεία : Ο(0,0) , Α1( , ) , Α2(- , -). Για τον χαρακτηρισμό αυτών των τριών σημείων, θα πρέπει να υπολογίσουμε την ποσότητα Δ=[fxy(x,y)]2-[fxx(x,y)][fyy(x,y)] στο κάθε σημείο.
Έχουμε fxx(x,y)=12x2 , fyy(x,y)=12y2 και fxy(x,y)=-8. Οπότε
Δ=(-8)2-12x212y2=64-144x2y2.
Στο σημείο Ο(0,0) : Δ=64>0 ΣΑΓΜΑΤΙΚΟ ΣΗΜΕΙΟ
Στο Α1( , ) : Δ=-512<0 και fxx(x,y)=24>0 ΤΟΠΙΚΟ ΕΛΑΧΙΣΤΟ
Στο Α2(- , -): Δ=-512<0 και fxx(x,y)=24>0 ΤΟΠΙΚΟ ΕΛΑΧΙΣΤΟ
Η τιμή του ελάχιστου είναι και στις δύο περιπτώσεις -8.

7. Να βρεθούν τα δεσμευμένα στάσιμα σημεία της συνάρτησης f(x,y)=1+x2+y2 με τον περιορισμό ότι τα (x,y) ικανοποιούν την εξίσωση Ακρότατα σημεία υπό περιορισμό
Απάντηση:
Στην παρούσα περίπτωση ο περιορισμός
μπορεί να λυθεί ως προς y, οπότε αντικαθιστώντας στην f(x,y)=1+x2+y2 έχουμε συνάρτηση μιας μόνο μεταβλητής της οποίας θα αναζητήσουμε τα στάσιμα σημεία.
Οι τιμές του x για τις οποίες μηδενίζεται η πρώτη παράγωγος 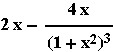είναι ρ1=- 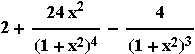, ρ2=0 , ρ3= . Η δεύτερη παράγωγος δίνει κατά σειράν τοπικό ελάχιστο, τοπικό μέγιστο, τοπικό ελάχιστο για την f(x,y)=1+x2+y2 με τον περιορισμό ότι τα (x,y) ικανοποιούν την εξίσωση .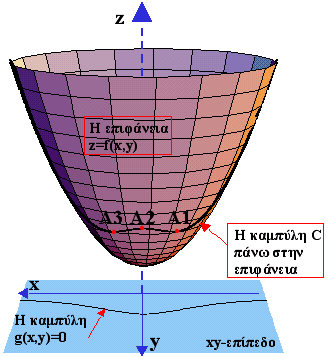


Στο σχήμα έχουμε την επιφάνεια z=f(x,y) , την καμπύλη πάνω στο xy-επίπεδο και την καμπύλη C που αποτελείται από τα σημεία της επιφάνειας που αντιστοιχούν στα ζεύγη (x,y) τα οποία ικανοποιούν την καμπύλη του περιορισμού.








8. Να βρεθούν τα δεσμευμένα στάσιμα σημεία της συνάρτησης f(x,y)=xy με τον περιορισμό x2/4+y2/2=1. Ακρότατα σημεία υπό περιορισμό
Απάντηση:
Η συνάρτηση f(x,y) και ο περιορισμός έχουν συνεχείς μερικές παραγώγους σε όλο το πεδίο ορισμού τους.Για την εύρεση των τοπικών ακρότατων της f(x,y) υπό τον περιορισμό θα εφαρμοσθεί η μέθοδος Lagrange.
Και έχουμε: fx(x,y)=y , fy(x,y)=x και gx(x,y)=x/2 , gy(x,y)=y
Σύμφωνα με το Θεώρημα 6.4
θα έχουμε το σύστημα { y=λx/2 , x=λy , x2/4+y2/2=1 }
Η λύση του συστήματος μας δίνει τα παρακάτω τέσσερα σημεία.
{ λ= , x1=, y1=1 } , { λ= , x2= -, y2= -1 },
{ λ= - , x3=, y3= -1 } , { λ= - , x4= -, y4=1 },
ή σαν σημεία επί της επιφανείας
Α( , 1 , ), Δ( - , -1 , ), Γ( , -1 , - ), Β(- , 1 , -)
όπου οι δύο πρώτες συντεταγμένες ικανοποιούν τον περιορισμό .
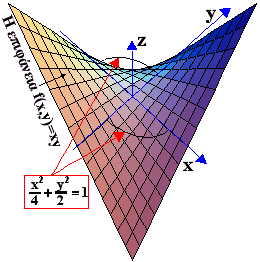Στο διπλανό σχήμα είναι η επιφάνεια, ο περιορισμός που είναι μια έλλειψη στο xy-επίπεδο και η οποία καλύπτεται εν μέρει από την επιφάνεια. Εάν κατά μήκος της έλλειψης φέρουμε κατακόρυφες ευθείες έτσι ώστε να τέμνουν την επιφάνεια θα δημιουργηθεί ένας κύλινδρος του οποίου η τομή με την επιφάνεια θα δώση μια τρισδιάστατη καμπύλη C. Η αναζήτηση των δεσμευμένων στάσιμων σημείων θα γίνει στα σημεία της C.


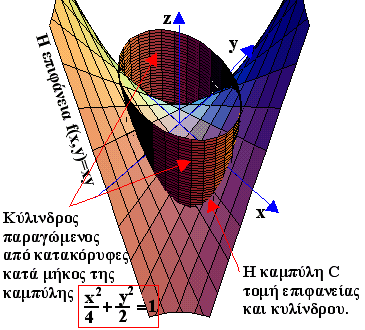Στο επόμενο σχήμα φαίνονται η επιφάνεια , και ο ελλειψοειδής κύλινδρος που τέμνει την επιφάνεια και δημιουργεί την καμπύλη C. Στο τρίτο σχήμα είναι η επιφάνεια , η έλλειψη του περιορισμού και η καμπύλη C με την παχύτερη γραμμή. Πάνω στην C έχουν σημειωθεί τα τέσσερα (κόκκινα) σημεία Α , Β , Γ , Δ που βρέθηκαν πιο πάνω με την μέθοδο Lagrange.


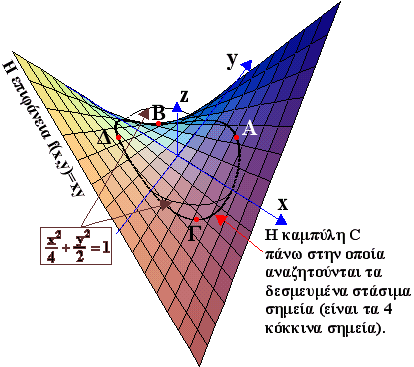Τα Α , Δ είναι σημεία τοπικού μέγιστου και τα Β , Γ σημεία τοπικού ελάχιστου. Ο χαρακτηρισμός των σημείων μπορεί να γίνει αν επιλύσουμε τον περιορισμό ως προς y (θα έχουμε δύο κλάδους) και αντικαταστήσουμε στην f(x,y)=xy.Θα γίνει συνάρτηση μιας μόνο μεταβλητής της οποίας τα στάσιμα σημεία προκύπτουν με την γνωστή διαδικασία για μονομεταβλητές συναρτήσεις.





9. Να βρεθούν τα ολικά ακρότατα των παρακάτω συναρτήσεων στις αντίστοιχες περιοχές : Ολικά ακρότατα 

a) z=x3+y3-9xy+23      ,        0 < x < 4    ,      0 < y < 4 
b) z=3+x3-x2-y2        ,      x2+y2 < 1    ,    x > 0.

Απάντηση:
a) Η συνάρτηση z=f(x,y)=x3+y3-9xy+23 είναι ορισμένη συνεχής και με συνεχείς παραγώγους στο xy-επίπεδο.Η περιοχή ( 0 < x < 4 , 0 < y < 4 ) που αναζητούνται τα ολικά ακρότατα είναι συμπαγής και η συνάρτηση συνεχής, επομένως υπάρχουν ακρότατα (Θεώρημα 6.5)
Πρώτο βήμα: Αναζήτηση ελεύθερων στάσιμων σημείων της z=x3+y3-9xy+23. Έχουμε zx=3x2-9y , zy=3y2-9x. Το σύστημα {3x2-9y=0 , 3y2-9x=0 } δίνει τα σημεία (0,0) και (3,3).
Δεύτερο βήμα : Αναζήτηση δεσμευμένων στάσιμων σημείων κατά μήκος του συνόρου της περιοχής.Το σύνορο αποτελείται από 4 καμπύλες (ευθύγραμμα τμήματα) που είναι:
AB: y=0 , f(x,0)=x3+23 , f΄=3x2=0 , και τελικά η κορυφή Α(0,0).
BD: x=4 , f(4,y)=y3-36y+87 , f΄=3y2-36=0 το σημείο Z(4,121/2)
DC: y=4 , f(y,4)=x3-36x+87 , f΄=3x2-36=0 το σημείο Η( 121/2,4)
CA: x=0 , f(0,y)=y3+23 , f΄=y2=0 , και τελικά η κορυφή Α(0,0).
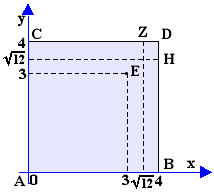Tρίτο βήμα : Προσδιορισμός των κορυφών, εδώ έχουμε τις Α(0,0), Β(4,0), D(4,4), C(0,4). Σύμφωνα με το Θεώρημα 6.6 θα πρέπει να εξετασθούν τα σημεία Α(0,0) , Β(4,0) , D(4,4) , C(0,4) , Ε(3,3) , Z(4 , 121/2) , H(121/2,4). Υπολογίζοντας τις τιμές έχουμε.
f(0,0)=23 , f(4,0)=87 , f(4,4)=7 , f(0,4)=87 , f(3,3)=-4 , f(4 , 121/2)=87-48(3)1/2 , f(121/2,4)=87-48(3)1/2.
Επομένως έχουμε δύο σημεία με μέγιστη τιμή τα Β(4,0) και C(0,4) και ένα σημείο με ελάχιστη το Ε(3,3).
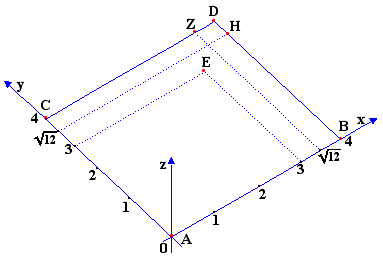Στο σχήμα φαίνονται τα επτά σημεία (με κόκκινο χρώμα) στα οποία θα υψωθούν κατακόρυφες ευθείες οι οποίες τέμνοντας την επιφάνεια f(x,y) προσδιορίζουν τα αντίστοιχα σημεία που εξετάζονται για τα ολικά ακρότατα.
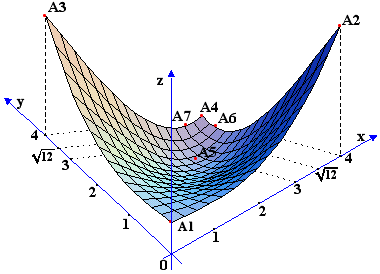Στο διπλανό σχήμα τα σημεία Α1,Α2,Α3,Α4,Α5,Α6,Α7 είναι τα σημεία που προκύπτουν από τις τομές της επιφάνειας με τις κατακόρυφες στα Α,Β,C,D,E,H,Z. Τα Α2 και Α3 αντιστοιχούν σε ολικό μέγιστο, και το Α5 σε ολικό ελάχιστο.







b) Η συνάρτηση z=f(x,y)=3+x3-x2-y2 είναι ορισμένη συνεχής και με συνεχείς παραγώγους σ'όλο το xy-επίπεδο, επομένως και στην περιοχή ( x2+y2 < 1 , x > 0 ) του xy-επιπέδου , που είναι το τμήμα του κυκλικού δίσκου με κέντρο την αρχή των αξόνων και ακτίνα 1 στο πρώτο και τέταρτο τεταρτημόριο. Η περιοχή είναι συμπαγής , επομένως υπάρχουν ακρότατα (Θεώρημα 6.5). Έχουμε :
1. Ελεύθερα στάσιμα σημεία :
fx=3x2-2x ,fy=-2y , Λύνοντας το σύστημα {3x2-2x=0 , -2y=0 } έχουμε τα σημεία (0,0) , (2/3,0) .

2. Δεσμευμένα στάσιμα σημεία :
Εδώ θα εξετασθούν οι δύο καμπύλες του συνόρου :
x=0 : f(0,y)=3-y2 , f΄(0,y)=-2y=0 , δηλαδή το σημείο (0,0).
y2=1-x2 : f(x,y(x))=x3+2 , f΄(x,y(x))=3x2 , x=0 οπότε έχουμε τα σημεία (0,-1) και (0,1).
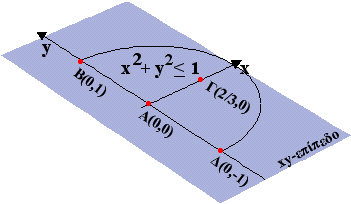3. Κορυφές :
Εδώ έχουμε δύο κορυφές τα σημεία (0,-1 , (0,1).
Οι τιμές της f(x,y) στα σημεία (0,0) , (2/3,0) , (0,-1) , (0,1) είναι f(0,0)=3, f(2/3,0)=77/27, f(0,-1)=2, f(0,1)=2. Σύμφωνα με το Θεώρημα 6.6 οι ολικές ακρότατες τιμές είναι: Μέγιστη τιμή 3 στo σημείο (0,0) και ελάχιστη τιμή 2 στα σημεία (0,-1) και (0,1).

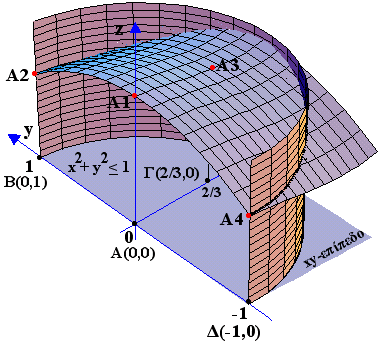Στο σχήμα τα σημεία Α1(0,0,3), Α2(2/3,0,77/27), Α3(1,0,3), Α4(0,1,2) είναι τα σημεία που αντιστοιχούν στα A, B, Γ, Δ. Κατά μήκος του τόξου ΒΔ υπάρχουν κατακόρυφες ευθείες που μαζύ με το κατακόρυφο επίπεδο κατά μήκος του y-άξονα (δεν απεικονίζεται) περικλείουν το εξεταζόμενο για ακρότατα σημεία τμήμα της επιφάνειας που καθορίζεται από τους περιορισμούς x2+y2 < 1 , x > 0.