και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθμός.
( Καρτεσιανή )
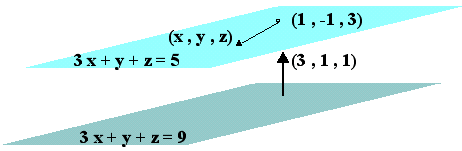
Ο αριθμός a δεν επιρρεάζει την λύση, οπότε η τυχαία τιμή a=9 επιλέχθηκε για το σχήμα.
Με ένα κάθετο διάνυσμα στο επίπεδο, το (3,1,1) και με το σημείο (1,-1,3) έχουμε ως καρτεσιανή εξίσωση του ζητουμένου επιπέδου την παρακάτω : 3x+y+z=3(1)+1(-1)+1(3)=5.
2)Ένα επίπεδο έχει εξίσωση x+2y+2z=4. Βρείτε :
(α) Την απόσταση της αρχής των αξόνων από το παραπάνω επίπεδο.
(β) Τις συντεταγμένες του σημείου Q του επιπέδου που έχει την ελάχιστη απόσταση από την αρχή Ο(ο,ο,ο).
( Παραμετρικές , Καρτεσιανή)
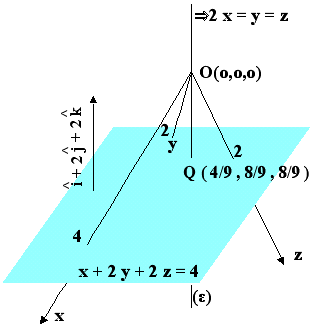
Θα βρεθεί η εξίσωση της ευθείας που περνά από την αρχή των αξόνων Ο(ο,ο,ο) και είναι κάθετη στο επίπεδο . Σε παραμετρική μορφή είναι x = t , y = 2t , z = 2t μια και το κάθετο διάνυσμα στο επίπεδο είναι (1,2,2). Η εξίσωση σε καρτεσιανή μορφή είναι με απαλοιφή του t 2x=y=z. Mαζύ με την εξίσωση του επιπέδου η λύση του συστήματος δίνει το κοινό σημείο τους Q(4/9,8/9,8/9). Τώρα η απόσταση της αρχής των αξόνων από το επίπεδο είναι το μήκος του διανύσματος |QΟ|=4/3.
Μια γενικώτερη αντιμετώπιση της απόστασης σημείου από επίπεδο είναι να υπολογισθεί η απόσταση ως το μήκος της προβολής του διανύσματος ΜΡο επάνω στο κάθετο διάνυσμα (A,B,C) στο επίπεδο Ax+By+Cz=D. Το Μ(x,y,z) είναι τυχαίο σημείο επί του επιπέδου.
3) Οι καρτεσιανές εξισώσεις τεσσάρων επιπέδων είναι
x+2y-2z=5 , 3x-6y+3z=3 , 2x+y+2z=-2 και x-2y+z=5.
(α) Δείξτε ότι δύο από αυτά είναι παράλληλα και τα άλλα δύο κάθετα.
(β) Υπολογίστε την απόσταση μεταξύ των παραλλήλων αυτών επιπέδων.
(Απόσταση σημείου από επίπεδο)
Τα κάθετα διανύσματα στα επίπεδα είναι αντιστοίχως (1,2,-2) , (3,-6,3) , (2,1,2) , (1,-2,1) και από τα οποία το πρώτο με το τρίτο έχουν εσωτερικό γινόμενο ίσο με το μηδέν {(1,1,2).(1,-2,1)=0} που σημαίνει ότι τα επίπεδα είναι κάθετα και το δεύτερο διάνυσμα είναι τριπλάσιο του τετάρτου {(3,-6,3)=3(1,-2,1)} που δηλώνει επίπεδα παράλληλα.
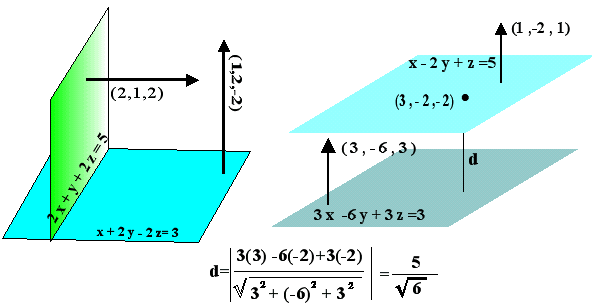
Για την απόσταση των επιπέδων παίρνουμε ένα σημείο του ενός επιπέδου και βρίσκουμε την απόσταση του από το άλλο επίπεδο όπως στην παραπάνω άσκηση . Ένα σημείο του x-2y+z=5 είναι το (3,-2,-2).
4)Βρείτε την εξίσωση για το επίπεδο που περιέχει τα σημεία
(2 , 3 , 5) , (1 , 5 , 6) και (-1 , 5 , 8) .
( Παραμετρικές , Καρτεσιανή )
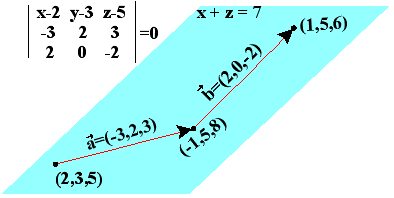
Τα δοθέντα σημεία ορίζουν 3 διανύσματα που βρίσκονται επάνω στο ζητούμενο επίπεδο. Δύο από αυτά είναι τα (-3,2,3) και (2,0,-2), που μαζύ με ένα από τα τρία σημεία, έστω το (2,3,5), δίνει τις παραμετρικές εξισώσεις x=2-3t+2m , y=3+2t , z=5+3t-2m .
H καρτεσιανή εξίσωση προκύπτει από την ορίζουσα που δίνει x+z=7.
5)Βρείτε την εξίσωση του επιπέδου που περιέχει το σημείο P(2 , 3 ,4)
και είναι κάθετο στην ευθεία
. ( Διανυσματική , Καρτεσιανή )
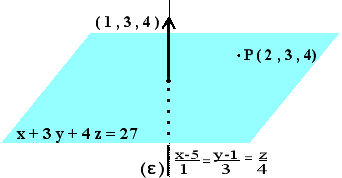Από
την εξίσωση της ευθείας έχουμε ένα διάνυσμα επί
της ευθείας το (1,3,4) οπότε η εξίσωση του επιπέδου
θα είναι 1x+3y+4z=D όπου το D θα υπολογισθεί από την
σχέση D=1(2)+3(3)+4(4)=27. Άρα το ζητούμενο επίπεδο είναι x+3y+4z=27.6)Βρείτε την ευθεία τομής των επιπέδων:
a) x+y+z=1 , x+y=3 , b) 3x-5y-2z=3 , 2x+3y-2z=3
( Παραμετρικές , Καρτεσιανή)
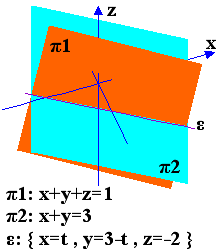
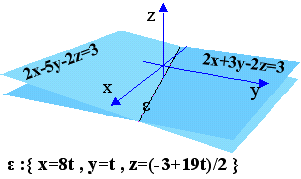
Η εξίσωση της ευθείας σε κάθε περίπτωση είναι το σύστημα των εξισώσεων των σχετικών επιπέδων. Για να βρούμε τις παραμετρικές εξισώσεις θέτουμε μια από τις (x,y,z) ίση με t και στη συνέχεια εκφράζουμε τις άλλες δύο συναρτήσει του t .
a) { x+y+z=1 , x+y=3 } , { x=t , y=3-t , z=-2 }
b) { 3x-5y-2z=3 , 2x+3y-2z=3 } , { x=8t , y=t , z=(-3+19t)/2 }
7)Αποδείξτε ότι η ευθεία x=3+t , y=2+2t , z=1+t είναι παράλληλη
προς το επίπεδο x-2y+3z=6. ( Εσωτερικό γινόμενο )
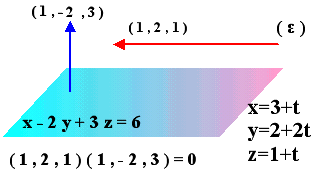Η
ευθεία για να είναι παράλληλη θα πρέπει να μην
έχει κοινό σημείο με το επίπεδο. Πράγματι το
σύστημα των εξισώσεων ευθείας και επιπέδου δεν
δίνει λύση που σημαίνει ότι η ευθεία είναι
παράλληλη προς το επίπεδο. Διαφορετικά
παρατηρούμε ότι το κάθετο διάνυσμα (1,-2,3) στο
επίπεδο και το διάνυσμα (1,2,1) επί της ευθείας
έχουν εσωτερικό γινόμενο μηδέν, δηλαδή το
διάνυσμα (1,2,1) είναι παράλληλο προς το επίπεδο άρα
και η ευθεία πάνω στην οποία βρίσκεται.
8)Να βρεθεί η εξίσωση του επιπέδου που είναι παράλληλο προς τον
y-άξονα και περνάει από την τομή των επιπέδων με εξισώσεις
x+2y+5z=4 και 2x-y+z=2. ( Καρτεσιανή )
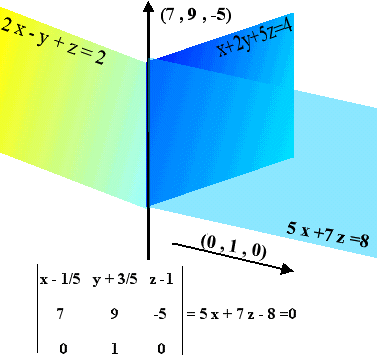Ένα διάνυσμα πάνω στον άξονα των y είναι το (0,1,0) και
ένα διάνυσμα επί της ευθείας είναι το (7,9,-5). Το
(7,9,-5) βρίσκεται αν δώσουμε στο z τις τιμές z=1, οπότε
έχουμε το σημείο (1/5,-3/5,1), και z=0 που δίνει το
σημείο (8/5,6/5,0). Με άκρα τα δύο σημεία έχουμε το
διάνυσμα (7/5,9/5,-1) ή το (7,9,-5). Η εξίσωση του επιπέδου
προκύπτει από την ορίζουσα που δίνει 5x+7z=8.
9)Να βρεθεί η γωνία που σχηματίζουν τα επίπεδα
x-y+2z=2 , 2x+y+z=3. ( Μέτρο διανύσματος , Εσωτερικό γινόμενο )
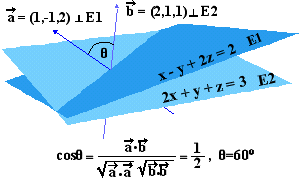Τα
κάθετα διανύσματα στα επίπεδα είναι (1,-1,2) και (2,1,1)
και η γωνία που σχηματίζουν είναι η γωνία των
επιπέδων. Με χρήση των εκφράσεων του εσωτερικού
γινομένου των δύο διανυσμάτων βρίσκουμε το cosθ
της γωνίας και στη συνέχεια την γωνία.
10)Η ευθεία (ε) διέρχεται από την αρχή των αξόνων και είναι κάθετη στο επίπεδο 2x-y-z=4.
Βρείτε το σημείο στο οποίο η (ε) τέμνει το επίπεδο x+y-2z=2.
( Παραμετρικές , Καρτεσιανή )
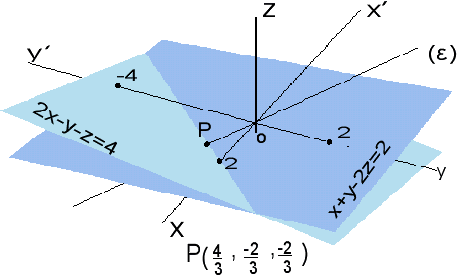
Η εξίσωση της ευθείας (ε) προσδιορίζεται από την αρχή Ο(ο,ο,ο) και από το κάθετο διάνυσμα στο επίπεδο 2x-y-z=4. Σε καρτεσιανή μορφή είναι {x=-y=-z} και σε παραμετρική μορφή {x=t , y=-t , z=-t}. Η επίλυση του συστήματος που αποτελείται από τις εξισώσεις της ευθείας και την εξίσωση του επιπέδου x+y-2z=2 δίνει τις συντεταγμένες του κοινού σημείου ευθείας και επιπέδου. Το σημείο Ρ έτυχε να έχει κοινό σημείο με το επίπεδο x+y-2z=2 επάνω στην κοινή ευθεία των δύο επιπέδων. Όπως και ο x-άξονας να τέμνει τα δύο επίπεδα στη κοινή τους ευθεία στο σημείο (2,0,0).