2.1 Περιγραφή διανυσμάτων στο χώρο
2.1.1 Γεωμετρική περιγραφή: Τα διανύσματα περιγράφονται σαν προσανατολισμένα ευθύγραμμα τμήματα.
Δύο διανύσματα θα θεωρούμε ότι είναι ίσα, εάν έχουν το ίδιο μήκος και την ίδια κατεύθυνση. Με άλλα λόγια θα θεωρούμε ένα διάνυσμα αμετάβλητο όταν κινείται παράλληλα προς τον εαυτόν του.
2.1.2 Αλγεβρική περιγραφή: Ένα διάνυσμα
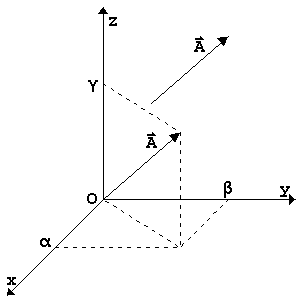
2.2 Mέτρο διανύσματος:
Το μέτρο ενός διανύσματος
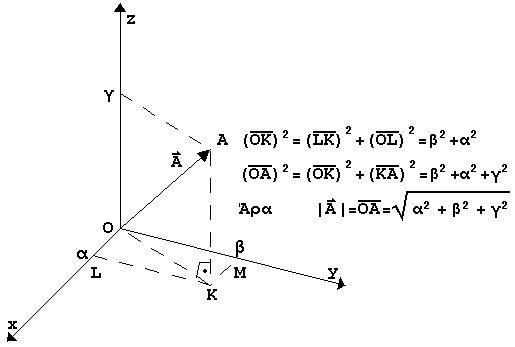
2.3 Κατευθύνοντα συνημίτονα
Έστω διάνυσμα
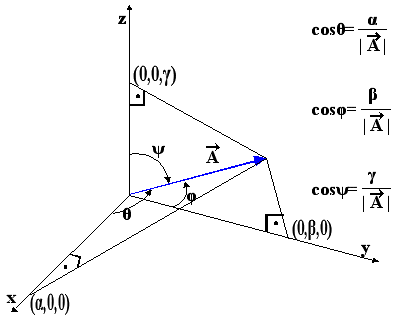
Τα συνημίτονα αυτά ονομάζονται κατευθύνοντα συνημίτονα του
2.4 Πράξεις
2.4.1 Πρόσθεση
Εάν
τότε
Γεωμετρική ερμηνεία πρόσθεσης
Γεωμετρικά το άθροισμα των
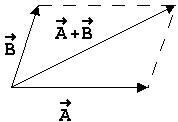 παραλληλογράμμου που έχει ως
προσκείμενες πλευρές του τα δύο διανύσματα
παραλληλογράμμου που έχει ως
προσκείμενες πλευρές του τα δύο διανύσματα 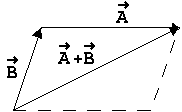 Εναλλακτικά
μπορούμε να τοποθετήσουμε το ένα διάνυσμα σαν
συνέχεια του άλλου, οπότε το άθροισμα βρίσκεται
ενώνοντας την αρχή του πρώτου με το πέρας του
δευτέρου.
Εναλλακτικά
μπορούμε να τοποθετήσουμε το ένα διάνυσμα σαν
συνέχεια του άλλου, οπότε το άθροισμα βρίσκεται
ενώνοντας την αρχή του πρώτου με το πέρας του
δευτέρου.
2.4.2 Πολλαπλασιασμός με αριθμό.
Εάν
τότε λ
Γεωμετρική ερμηνεία πολλαπλασιασμού.
Το διάνυσμα λ
Επίσης θα έχουμε ότι |λ
2.4.3 Αφαίρεση
Εάν
2.4.4 Εσωτερικό γινόμενο
Έστω μη-μηδενικά διανύσματα
Το εσωτερικό γινόμενο συμβολίζεται με
Γεωμετρική ερμηνεία εσωτερικού γινομένου.
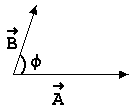
Παρατήρηση:
2.5 Μοναδιαία διανύσματα.
Διανύσματα που έχουν μέτρο 1.
Συνήθως συμβολίζονται με
Παρατήρηση: Εάν
είναι μοναδιαίο και έχει την ίδια κατεύθυνση με το
(Τα cosθ,cosφ,cosψ είναι τα κατευθύνοντα συνημίτονα του
2.6 Βασικά διανύσματα.
Είναι τα
2.7 Προβολή
Αν
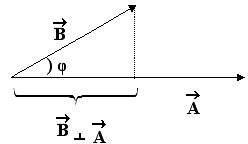 Σημειωτέον ότι η προβολή είναι προσημασμένη , και
είναι θετική ή αρνητική αν η γωνία είναι οξεία ή
αμβλεία αντίστοιχα.
Σημειωτέον ότι η προβολή είναι προσημασμένη , και
είναι θετική ή αρνητική αν η γωνία είναι οξεία ή
αμβλεία αντίστοιχα.
Παρατήρηση :
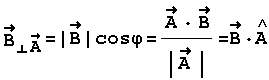 .
.2.8 Παράλληλα διανύσματα.
Έστω
Χρησιμοποιώντας την γεωμετρική ερμηνεία της πράξης του πολλαπλασιασμού με αριθμό , παρατηρούμε ότι: Δύο παράλληλα διανύσματα τοποθετημένα με την ίδια αρχή βρίσκονται πάνω στην ίδια ευθεία. Για το λόγο αυτό δύο παράλληλα διανύσματα ονομάζονται συγγραμμικά.
2.9 Συνεπίπεδα διανύσματα.
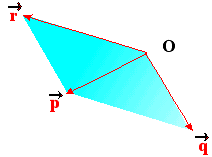
Δύο μη-συγγραμμικά διανύσματα
Ένα διάνυσμα
(a): Μπορεί να εκφρασθεί σαν γραμμικός συνδυασμός τους, δηλαδή μπορεί να εκφρασθεί στην μορφή:
(b):
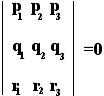
Δηλαδή μηδενίζεται η ορίζουσα των συντεταγμένων των τριών διανυσμάτων.