Να βρεθεί η εξίσωση της ευθείας (ε) σε καρτεσιανή ,
παραμετρική και διανυσματική μορφή.
(Διανυσματική,Παραμετρική,Καρτεσιανή).Απάντηση
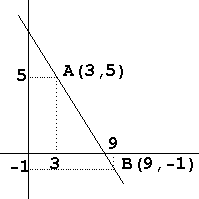Η ζητούμενη ευθεία θα είναι
παράλληλη προς το διάνυσμα ΒΑ=(-6,6) .Η διανυσματική της εξίσωσι : ΑΜ=tBA.
Παραμετρικές εξισώσεις : Παίρνοντας το Β
που είναι σημείο της ζητούμενης ευθείας ,
θα έχουμε x=9+(-6)t , y=-1+6t.
Η καρτεσιανή εξίσωση είναι x+y=8.
2. Μια ευθεία (ε) διέρχεται από το σημείο Α(0,-2) με κλίση 2 .
Να βρεθεί η καρτεσιανή εξίσωση της (ε).
(Κλίση).Απάντηση
Από την εξίσωση Αx+By=C για κάθε σημείο
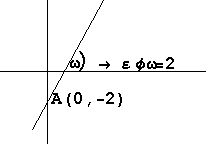
της ευθείας έχουμε ότι Axo+Byo=C.
Αφαιρούμε κατά μέλη και έχουμε :
A(x-xo)+B(y-yo)=0.
Με k=-A/B και με Β διάφορο του μηδενός , τελικά έχουμε y-yo=k(x-xo ).
Για xo=0 και yo=- 2 η καρτεσιανή εξίσωση είναι 2x-y=2.
3. Να βρεθεί η καρτεσιανή εξίσωση της ευθείας που είναι
παράλληλη προς την ευθεία , που διέρχεται από τα σημεία
Α(-5,7) και Β(2,0) και περνάει από το σημείο Γ(1,5).
(Καρτεσιανή).Απάντηση
H ευθεία που περνά από τα Α , Β περιέχει.
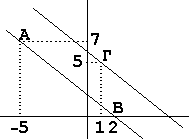
και το διάνυσμα ΑΒ=(2-(-5),0-7)=(7,-7)
Οπότε η ζητούμενη περνά από το Γ(1,5)
και είναι παράλληλη στο διάνυσμα (7,-7).
Η καρτεσιανή της εξίσωση είναι
-7(x-1)-7(y-5)=0 ή x+y=6
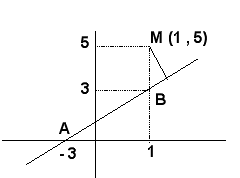
4. Να υπολογισθεί η απόσταση του σημείου Μ(1,5) από την
ευθεία που διέρχεται από τα σημεία Α(1,3) και Β(-3,0).
Γενικώτερα να βρεθεί ο τύπος που δίνει την απόσταση ενός
σημείου Po(xo,yo) από μια ευθεία (ε) με εξίσωση Ax+By=C.
(Καρτεσιανή , Εσωτερικό γινόμενο διανυσμάτων , Προβολή διανύσματος σε διάνυσμα) . Απάντηση Η απόσταση σημείου από ευθεία μπορεί να βρεθεί , αν βρούμε την εξίσωση της ευθείας που περνά από το σημείο και είναι κάθετη προς την αρχική ευθεία και στην συνέχεια να προσδιορίσουμε το σημείο τομής των δύο ευθειών , λύνοντας το σύστημα , και κατόπιν υπολογίζοντας την μεταξύ των δύο σημείων απόσταση.
Ένας άλλος τρόπος είναι να προσδιορισθεί το μήκος της προβολής ενός τυχαίου διανύσματος (που έχει άκρα το δοθέν σημείο και ένα τυχαίο σημείο επί της ευθείας) επάνω στο κάθετο διάνυσμα στην δοθείσα ευθεία.
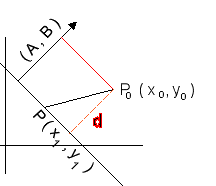
Το διάνυσμα (Α,Β) είναι κάθετο στην ευθεία Ax+By=C.
Έστω τυχαίο σημείο της ευθείας P(x1,x2).
Τότε το διάνυσμα PPo=(xo-x1,yo-y1) έχει μήκος προβολής επάνω στο (Α,Β) ίση με την απόσταση του Po(xo,yo) από την ευθεία Ax+By=C.
Μήκος προβολής=|(xo-x1,yo-y1)(Α,Β)(Α,Β)/(Α,Β)(Α,Β)|=
|Αxo-Ax1+Byo-By1|/|(A,B)| ή |Axo+Byo-C|/|(A,B)|.
Εφαρμογή στην άσκηση :
Η εξίσωση της ευθείας είναι 3x-4y=-9. Το κάθετο διάνυσμα σε αυτήν είναι (3,-4).
Το δοθέν σημείο είναι (1,5) και βάσει του προηγουμένου αποτελέσματος η απόσταση είναι |3.1+(-4).5 - (-9)| / 5=8/5
5. Να γραφούν οι σχέσεις που ικανοποιούν τα σημεία από τις
παρακάτω δύο σκιαγραφημένες περιοχές.
(Ημιεπίπεδα) . Απάντηση
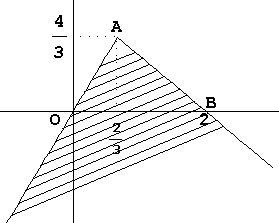
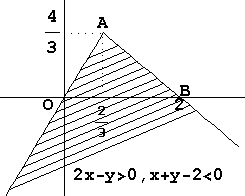
Στο πρώτο σχήμα η ευθεία ΑΟ είναι 2x-y=0 και η ΑΒ είναι x+y-2=0.
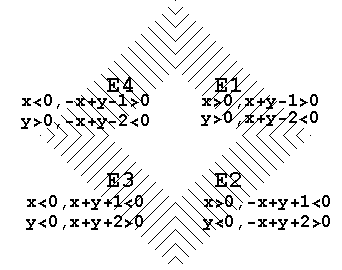
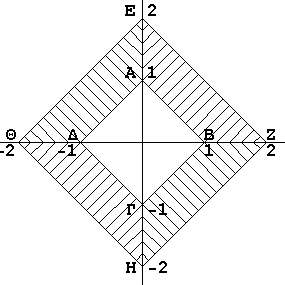
Στο δεύτερο σχήμα κάθε περιοχή περικλείεται από 4 ευθείες .
Ε1: x=0 , y=0 , x+y-1=0 , x+y-2=0
E2: x=0 , y=0 ,-x+y+1=0 , -x+y+2=0
E3: x=0 , y=0 , x+y+1=0 , x+y+2=0
E4: x=0 , y=0 ,-x+y-1=0 , -x+y-2=0
Στο σχήμα είναι και οι σχέσεις που προσδιορίζουν την κάθε περιοχή. Σε όλες τις περιπτώσεις οι καρτεσιανές εξισώσεις των ευθειών βρέθηκαν από τα δύο σημεία από τα οποία περνά η καθεμιά όπως στην άσκηση 1.