Πόρισμα 3.2 :
Έστω γραμμικό σύστημα Α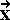 =
= 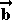 m εξισώσεων με n μεταβλητές . Το Α
m εξισώσεων με n μεταβλητές . Το Α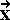 =
= 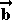 είναι συμβατό εάν μόνον εάν ο επαυξημένος πίνακας ( Α :
είναι συμβατό εάν μόνον εάν ο επαυξημένος πίνακας ( Α : 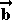 ) έχει τον ίδιο βαθμό με τον πίνακα των συντελεστών Α.
) έχει τον ίδιο βαθμό με τον πίνακα των συντελεστών Α.
Απόδειξη
Έστω  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n τα διανύσματα στηλών του Α.
n τα διανύσματα στηλών του Α.
Προφανώς οι υπόχωροι L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) , L(
n ) , L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ,
n , 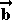 ) του
) του  m θα ταυτίζονται με τους στηλοχώρους των πινάκων Α και ( Α :
m θα ταυτίζονται με τους στηλοχώρους των πινάκων Α και ( Α : 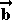 ) είναι συμβατό εάν και μόνον εάν το
) είναι συμβατό εάν και μόνον εάν το 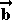 ανήκει στον στηλόχωρο του Α, εάν δηλαδή
ανήκει στον στηλόχωρο του Α, εάν δηλαδή 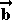
 L(
L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) .
n ) .
Όμως από την άσκηση 8 του Κεφαλαίου 2 , 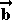
 L(
L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) εάν και μόνον εάν L(
n ) εάν και μόνον εάν L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) = L(
n ) = L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ,
n , 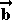 )
Επειδή L(
)
Επειδή L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n )
n ) 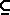 L(
L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ,
n , 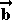 ) από το Θεώρημα 2.5 προκύπτει ότι : L(
) από το Θεώρημα 2.5 προκύπτει ότι : L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) = L(
n ) = L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ,
n , 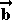 ) εάν και μόνον εάν dim( L(
) εάν και μόνον εάν dim( L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) ) = dim( L(
n ) ) = dim( L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ,
n , 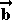 ) )
Όμως οι διαστάσεις των στηλοχώρων των πινάκων Α και ( Α :
) )
Όμως οι διαστάσεις των στηλοχώρων των πινάκων Α και ( Α : 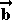 ) ταυτίζονται με τους βαθμούς αυτών των πινάκων.
) ταυτίζονται με τους βαθμούς αυτών των πινάκων.
Άρα L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ) = L(
n ) = L(  1 ,
1 ,  2 , . . . ,
2 , . . . ,  n ,
n , 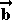 )
εάν και μόνον εάν οι πίνακες Α και ( Α :
)
εάν και μόνον εάν οι πίνακες Α και ( Α : 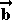 ) έχουν τον ίδιο βαθμό.
) έχουν τον ίδιο βαθμό.
Επομένως , το σύστημα Α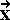 =
= 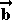 είναι συμβατό εάν και μόνον εάν ο επαυξημένος πίνακας ( Α :
είναι συμβατό εάν και μόνον εάν ο επαυξημένος πίνακας ( Α : 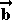 ) έχει τον ίδιο βαθμό με τον πίνακα συντελεστών Α.
) έχει τον ίδιο βαθμό με τον πίνακα συντελεστών Α.