(a) Έλλειψη με κέντρο στο (- 2 ,3) , μεγάλο άξονα παράλληλο προς τον y-άξονα μήκους 10 και μήκος μικρού άξονα 6.
(b) Παραβολή με εστία στο (4,3) και διευθετούσα ευθεία την y+1=0.
(c) Υπερβολή με κέντρο στο (1,1) εστία στο (6,1) και κορυφή στο (4,1).
Απαντήσεις
1(a)
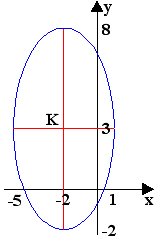
Εφ'όσον ο μεγάλος άξονας της έλλειψης είναι παράλληλος προς τον y-άξονα τότε η εξίσωση της έλλειψης θα είναι της μορφής 5.18 και είναι η
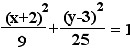 .
.
1(b)
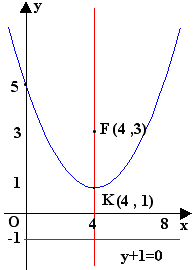
Η παραβολή που περιγράφεται από τα δοθέντα στοιχεία έχει τον άξονά της παράλληλο προς τον y-άξονα , οπότε έχει το σχήμα που αντιστοιχεί στην εξίσωση της μορφής 5.13 , όπως φαίνεται από την διάταξη της εστίας F(4,3), της κορυφής K(4,1) και της διευθετούσης y+1=0, η ζητούμενη εξίσωση έχει c>0 και είναι (x-4)2=4(2)(y-1).
1(c)
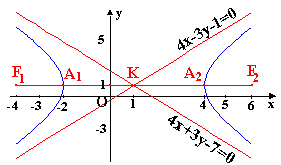 Η υπερβολή που περιγράφεται από
τα δοθέντα στοιχεία έχει τις εστίες της F1(-4,1) & F2(6,1),
τις κορυφές της A1(-2,1) & A2(4,1) και το κέντρο της K(1,1) σε μια ευθεία την y=1 παράλληλη προς τον x-άξονα. Οπότε η
εξίσωσή της θα είναι της μορφής 5.19
και είναι
Η υπερβολή που περιγράφεται από
τα δοθέντα στοιχεία έχει τις εστίες της F1(-4,1) & F2(6,1),
τις κορυφές της A1(-2,1) & A2(4,1) και το κέντρο της K(1,1) σε μια ευθεία την y=1 παράλληλη προς τον x-άξονα. Οπότε η
εξίσωσή της θα είναι της μορφής 5.19
και είναι 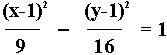
2) Να χαρακτηριστούν οι παρακάτω κωνικές τομές και να δοθεί η γραφική τους παράσταση:
(a) 4x2+9y2-40x+36y+100=0 , (b) 9x2-16y2-54x-64y-127=0 , (c)32x2+52xy-7y2+180=0 , (d) xy=-2 , (e) 3x2+10xy+3y2-2x-14y-13=0 , (f) 9x2-24xy+16y2-20x+110y=50.
Απαντήσεις
2(a)
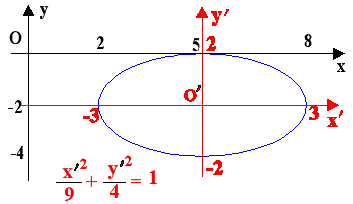 Η εξίσωση 4x2+9y2-40x+36y+100=0
δεν έχει τον όρο xy και έχοντας αγ=(4)(9)=36>0
περιγράφει έλλειψη (σε ειδική
περίπτωση περιγράφει ή ένα σημείο ή κανένα
γεωμετρικό σχήμα). Με παράλληλη
μετατόπιση αξόνων, στο σημείο Ο'(5,-2)
, η εξίσωση πέρνει την μορφή
x'2/9+y'2/4=1.
Η τελευταία εξίσωση περιγράφει έλλειψη με κέντρο
τη νέα αρχή των αξόνων
Ο' και μήκος μεγάλου της
άξονα 6 και μικρού 4.
Η εξίσωση 4x2+9y2-40x+36y+100=0
δεν έχει τον όρο xy και έχοντας αγ=(4)(9)=36>0
περιγράφει έλλειψη (σε ειδική
περίπτωση περιγράφει ή ένα σημείο ή κανένα
γεωμετρικό σχήμα). Με παράλληλη
μετατόπιση αξόνων, στο σημείο Ο'(5,-2)
, η εξίσωση πέρνει την μορφή
x'2/9+y'2/4=1.
Η τελευταία εξίσωση περιγράφει έλλειψη με κέντρο
τη νέα αρχή των αξόνων
Ο' και μήκος μεγάλου της
άξονα 6 και μικρού 4.2(b)
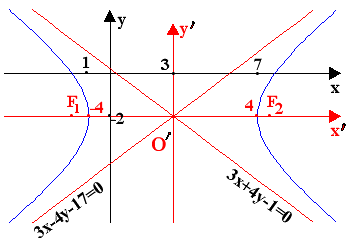 Η δοθείσα εξίσωση 9x2-16y2-54x-64y-127=0 δεν έχει
τον όρο xy και έχει αγ=(9)(-16)=-144<0 οπότε περιγράφει υπερβολή (ή σε ειδική περίπτωση
ένα ζεύγος τεμνομένων ευθειών). Με παράλληλη μετατόπιση των αξόνων,
στο σημείο Ο'(3,-2) , η εξίσωση
πέρνει την μορφή x'2/16-y'2/9=1.
Η τελευταία εξίσωση περιγράφει υπερβολή με
κέντρο την αρχή Ο' των νέων αξόνων και κορυφές τα
σημεία (-4,0) και (4,0) στο νέο σύστημα αξόνων. Οι εξισώσεις των ασυμπτώτων
(3x-4y-17=0 , 3x+4y-1=0) στο σχήμα αναφέρονται στο αρχικό
σύστημα αξόνων.
Η δοθείσα εξίσωση 9x2-16y2-54x-64y-127=0 δεν έχει
τον όρο xy και έχει αγ=(9)(-16)=-144<0 οπότε περιγράφει υπερβολή (ή σε ειδική περίπτωση
ένα ζεύγος τεμνομένων ευθειών). Με παράλληλη μετατόπιση των αξόνων,
στο σημείο Ο'(3,-2) , η εξίσωση
πέρνει την μορφή x'2/16-y'2/9=1.
Η τελευταία εξίσωση περιγράφει υπερβολή με
κέντρο την αρχή Ο' των νέων αξόνων και κορυφές τα
σημεία (-4,0) και (4,0) στο νέο σύστημα αξόνων. Οι εξισώσεις των ασυμπτώτων
(3x-4y-17=0 , 3x+4y-1=0) στο σχήμα αναφέρονται στο αρχικό
σύστημα αξόνων.
2(c)
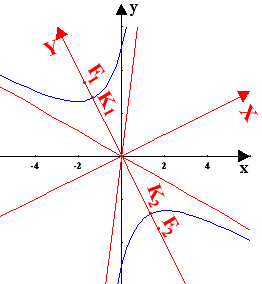
Στην εξίσωση 32x2+52xy-7y2+180=0 είναι 4αγ-β2= -3600<0 οπότε πρόκειται περί υπερβολής (ή σε ειδική περίπτωση ένα ζεύγος τεμνομένων ευθειών). Καθώς περιέχει τον όρο xy για τη απαλοιφή του χρειάζεται περιστροφή αξόνων.
Εδώ έχουμε tan2θ=4/3 ή tanθ=1/2 δηλ.
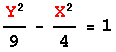 .
Η τελευταία εξίσωση περιγράφει
υπερβολή με κέντρο την αρχή των αξόνων και με κορυφές -εστίες στο νέο σύστημα αξόνων τα σημεία:
.
Η τελευταία εξίσωση περιγράφει
υπερβολή με κέντρο την αρχή των αξόνων και με κορυφές -εστίες στο νέο σύστημα αξόνων τα σημεία:2(d)
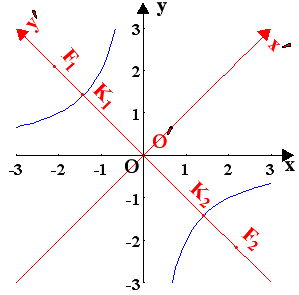 Η εξίσωση xy=-2 έχει τον
όρο xy και 4αγ-β2=-1<0
οπότε περιγράφει υπερβολή .
Εδώ είναι θ=π/4 και με περιστροφή
των αξόνων , βάσει των σχέσεων
(5.5) ,η εξίσωση πέρνει την μορφή
Η εξίσωση xy=-2 έχει τον
όρο xy και 4αγ-β2=-1<0
οπότε περιγράφει υπερβολή .
Εδώ είναι θ=π/4 και με περιστροφή
των αξόνων , βάσει των σχέσεων
(5.5) ,η εξίσωση πέρνει την μορφή 2(e)
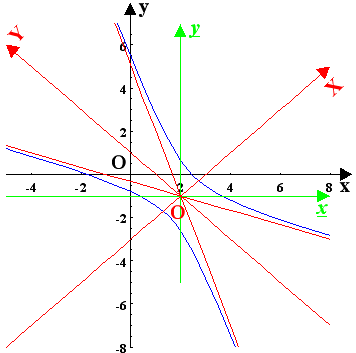 Η δοθείσα εξίσωση 3x2+10xy+3y2-2x-14y-13=0
περιέχει τον όρο xy και είναι 4αγ-β2=-64<0
οπότε περιγράφει μια υπερβολή
(ή σε ειδική περίπτωση ένα ζεύγος
τεμνομένων ευθειών).
Η δοθείσα εξίσωση 3x2+10xy+3y2-2x-14y-13=0
περιέχει τον όρο xy και είναι 4αγ-β2=-64<0
οπότε περιγράφει μια υπερβολή
(ή σε ειδική περίπτωση ένα ζεύγος
τεμνομένων ευθειών).Πρώτα με παράλληλη μετατόπιση των αξόνων στο σημείο (2,-1) βάσει των σχέσεων (5.2) έχουμε την εξίσωση 3x2+10xy+3y2-8=0 και με περιστροφή των αξόνων που προέκυψαν κατά γωνία θ=π/4 βάσει των σχέσεων (5.5) έχουμε την τελική εξίσωση Χ2-Υ2/4=1ως προς το σύστημα YOX. Η τελευταία εξίσωση περιγράφει υπερβολή με κέντρο , εστίες , κορυφές επάνω στον άξονα ΟΧ . Οι εξισώσεις των ασυμπτώτων ως προς το αρχικό σύστημα αξόνων είναι { 3x+y-5=0 , x+3y+1=0 }.
2(f)
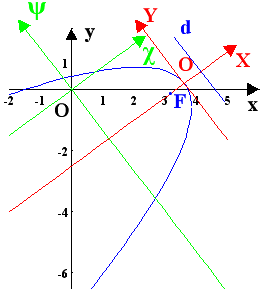 Ηδοθείσα εξίσωση 9x2-24xy+16y2-20x+110y=50 έχει 4αγ-β2=0
οπότε περιγράφει παραβολή (σε
ειδική περίπτωση ένα ζεύγος παραλλήλων ευθείων
που συμπίπτουν ή δεν συμπίπτουν ή κανένα
γεωμετρικό σχήμα). Στην περίπτωση της παραβολής
πρώτα περιστρέφουμε τους
άξονες και στη συνέχεια τους μεταφέρουμε
παράλληλα. Εδώ από την σχέση tan2θ=β/(α-γ)=24/7
βρίσκουμε ότι cosθ=4/5 , sinθ=3/5 και βάσει των σχέσεων (5.5) αντικαθιστόντας
στην αρχική έχουμε την εξίσωση (ψ+2)2=-2(χ-3) ως προς το σύστημα αξόνων ψΟχ .Τώρα παράλληλη
μεταφορά των αξόνων δίνει την εξίσωση Y2=-2X ως προς το
σύστημα αξόνων ΥΟΧ. Η τελευταία περιγράφει
παραβολή με κορυφή την αρχή Ο των αξόνων και άξονά της τον ΟΧ .
Η κορυφή της ως προς τους αρχικούς άξονες είναι (3.6 , 0.2). Εξίσωση της
διευθετούσας d ως
προς τους αρχικούς είναι η 8x+6y=35 και η εστία F έχει συντεταγμένες (3.2 ,
-0.2).
Ηδοθείσα εξίσωση 9x2-24xy+16y2-20x+110y=50 έχει 4αγ-β2=0
οπότε περιγράφει παραβολή (σε
ειδική περίπτωση ένα ζεύγος παραλλήλων ευθείων
που συμπίπτουν ή δεν συμπίπτουν ή κανένα
γεωμετρικό σχήμα). Στην περίπτωση της παραβολής
πρώτα περιστρέφουμε τους
άξονες και στη συνέχεια τους μεταφέρουμε
παράλληλα. Εδώ από την σχέση tan2θ=β/(α-γ)=24/7
βρίσκουμε ότι cosθ=4/5 , sinθ=3/5 και βάσει των σχέσεων (5.5) αντικαθιστόντας
στην αρχική έχουμε την εξίσωση (ψ+2)2=-2(χ-3) ως προς το σύστημα αξόνων ψΟχ .Τώρα παράλληλη
μεταφορά των αξόνων δίνει την εξίσωση Y2=-2X ως προς το
σύστημα αξόνων ΥΟΧ. Η τελευταία περιγράφει
παραβολή με κορυφή την αρχή Ο των αξόνων και άξονά της τον ΟΧ .
Η κορυφή της ως προς τους αρχικούς άξονες είναι (3.6 , 0.2). Εξίσωση της
διευθετούσας d ως
προς τους αρχικούς είναι η 8x+6y=35 και η εστία F έχει συντεταγμένες (3.2 ,
-0.2).3) Να βρεθεί η εξίσωση της παραβολής που έχει την x+y-2=0 διευθετούσα ευθεία της και της οποίας η εστία ταυτίζεται με την αρχή των αξόνων.
Απάντηση
Kef5.gif) Από τα δεδομένα του
προβλήματος και το Σχ.1 έχουμε ότι η ζητούμενη
παραβολή θα έχει ως εστία το σημείο F
που είναι συγχρόνως και η αρχή των αξόνων ως προς
τους οποίους ζητείται η εξίσωση της παραβολής
και κορυφή το σημείο Κ , το μέσον
της απόστασης της εστίας F από την διευθετούσα
. Η ευθεία y=x περνά από την εστία και είναι κάθετη
στην x+y-2=0 (d) που είναι η
διευθετούσα της παραβολής. Έτσι βρίσκουμε τις
συντεταγμένες του Κ ότι είναι
(1/2,1/2) και την απόσταση του Κ από
την εστία F ότι είναι
Από τα δεδομένα του
προβλήματος και το Σχ.1 έχουμε ότι η ζητούμενη
παραβολή θα έχει ως εστία το σημείο F
που είναι συγχρόνως και η αρχή των αξόνων ως προς
τους οποίους ζητείται η εξίσωση της παραβολής
και κορυφή το σημείο Κ , το μέσον
της απόστασης της εστίας F από την διευθετούσα
. Η ευθεία y=x περνά από την εστία και είναι κάθετη
στην x+y-2=0 (d) που είναι η
διευθετούσα της παραβολής. Έτσι βρίσκουμε τις
συντεταγμένες του Κ ότι είναι
(1/2,1/2) και την απόσταση του Κ από
την εστία F ότι είναι Kef5.gif) Από το Σχ.2 και τα
δεδομένα η εξίσωση της παραβολής ως προς το
σύστημα yKx θεωρουμένη θα είναι y2=-4
Από το Σχ.2 και τα
δεδομένα η εξίσωση της παραβολής ως προς το
σύστημα yKx θεωρουμένη θα είναι y2=-4Kef5.gif)
Kef5.gif)
4) Να βρεθούν οι εξισώσεις των ελλείψεων και υπερβολών που έχουν το κέντρο τους στην αρχή των αξόνων και τον έναν άξονα στην ευθεία x=y.
Απάντηση
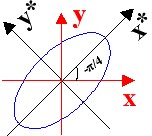 Παίρνουμε ως
σύστημα αξόνων x*Oy* το ταυτιζόμενο
με τους άξονες της έλλειψης , τότε θα έχουμε ως
εξίσωση της:
Παίρνουμε ως
σύστημα αξόνων x*Oy* το ταυτιζόμενο
με τους άξονες της έλλειψης , τότε θα έχουμε ως
εξίσωση της: 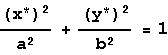 . Ο άξονας Οx*έχοντας
εξίσωση y=x ως προς το σύστημα αξόνων xOy
σχηματίζει γωνία με τον άξονα Ox ίση με
. Ο άξονας Οx*έχοντας
εξίσωση y=x ως προς το σύστημα αξόνων xOy
σχηματίζει γωνία με τον άξονα Ox ίση με 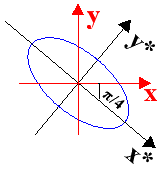 Εάν ήταν ο άλλος άξονας
επάνω στην ευθεία x=y τότε η γωνία είναι π/4 και
η εξίσωση των ελλείψεων είναι
Εάν ήταν ο άλλος άξονας
επάνω στην ευθεία x=y τότε η γωνία είναι π/4 και
η εξίσωση των ελλείψεων είναι 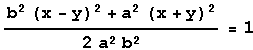 .
.Αντιστοίχως για τις υπερβολές θα έχουμε από την εξίσωση
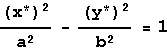 τα
σχήματα
τα
σχήματα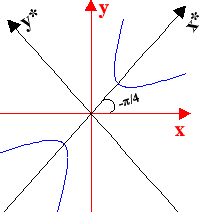
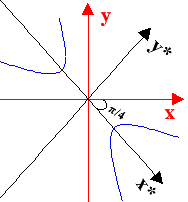
με αντίστοιχες εξισώσεις
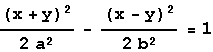 ,
, 5) Να βρεθούν οι εξισώσεις των παραβολών που έχουν την κορυφή τους στο σημείο (1,-2) και άξονα παράλληλο προς την ευθεία y=x.
Απάντηση
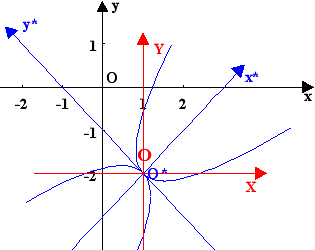 Οι περιγραφόμενες
παραβολές δίνονται από την εξίσωση x*=a
(y*)2 ,
όπου το a είναι πραγματικός αριθμός , ως
σύστημα συντεταγμένων έχουμε το y*O*x* , όπου O*x* είναι ο
άξονας των παραβολών και O*y* είναι
η ευθεία που διέρχεται από την κορυφή (1,-2) των
παραβολών και είναι κάθετος στον
O*x*. Ο
άξονας O*x* έχει εξίσωση y=x-3 ως προς το σύστημα yOx και για να γίνει παράλληλος προς τον άξονα Ox θα
πρέπει να στραφεί κατά γωνία -π/4 . Βάσει των σχέσεων (5.5) έχουμε μετά την
περιστροφή την εξίσωση (X+Y)/
Οι περιγραφόμενες
παραβολές δίνονται από την εξίσωση x*=a
(y*)2 ,
όπου το a είναι πραγματικός αριθμός , ως
σύστημα συντεταγμένων έχουμε το y*O*x* , όπου O*x* είναι ο
άξονας των παραβολών και O*y* είναι
η ευθεία που διέρχεται από την κορυφή (1,-2) των
παραβολών και είναι κάθετος στον
O*x*. Ο
άξονας O*x* έχει εξίσωση y=x-3 ως προς το σύστημα yOx και για να γίνει παράλληλος προς τον άξονα Ox θα
πρέπει να στραφεί κατά γωνία -π/4 . Βάσει των σχέσεων (5.5) έχουμε μετά την
περιστροφή την εξίσωση (X+Y)/