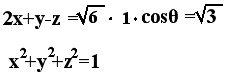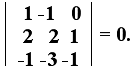Απαντήσεις ασκήσεων
2ου Κεφαλαίου
1. Θεωρούμε
τα διανύσματα 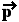 =
=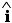 +2
+2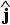 +
+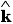 και
και 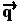 =2
=2 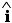 +
+ 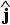 +2
+2 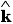 . Να βρεθεί ένα
διάνυσμα
. Να βρεθεί ένα
διάνυσμα 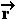 με την εξής
ιδιότητα: εάν θεωρήσουμε ότι τα
με την εξής
ιδιότητα: εάν θεωρήσουμε ότι τα 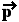 ,
, 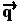 ,
, 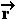 έχουν
για αρχή τους ,την αρχή των αξόνων, τότε τα πέρατα
των
έχουν
για αρχή τους ,την αρχή των αξόνων, τότε τα πέρατα
των 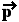 ,
,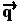 ,
, 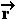 να αποτελούν κορυφές
ενός ορθογωνίου τριγώνου.
να αποτελούν κορυφές
ενός ορθογωνίου τριγώνου.
(Εσωτερικό γινόμενο , Πρόσθεση , Αφαίρεση)
Τα δύο διανύσματα που δίνονται ορίζουν τα σημεία
Α και Β.Έστω ότι το ζητούμενο τρίτο διάνυσμα
ορίζει ένα σημείο Γ. H ορθή γωνία μπορεί να είναι
σ'ένα από τα Α,Β,Γ. Έστω στο Β. Εάν το Γ έχει
συντεταγμένες (x,y,z) θα είναι το εσωτερικό
γινόμενο των διανυσμάτων (ΑΒ).(BΓ)=0. Από την
σχέση αυτή έχουμε (1,-1,1).(x-2,y-1,z-2)=0 ή x-2-y+1+z-2=0 ή
x-y+z=3. Η τελευταία ισότητα αληθεύει για άπειρες
τριάδες (x,y,z) μια από αυτές είναι (3,0,0). Επομένως
μια λύση είναι 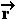 =(3,0,0).
Γενικεύοντας παρατηρούμε ότι το Γ βρίσκεται
σ'ένα επίπεδο κάθετο στο διάνυσμα ΑΒ στο σημείο Β.
Η εξίσωσή του είναι 1x-1y+1z=1.2+(-1).1+1.2
ή x-y+z=3. Οιοδήποτε σημείο του επιπέδου αυτού είναι
λύση. Αν η ορθή γωνία ήταν στο Α θα έχουμε επίπεδο
κάθετο στο ΑΒ στο Α και παράλληλο προς το
προηγούμενο με εξίσωση x-y+z=0. Τα σημεία Α,Β,Ο
εξαιρούνται διότι δεν έχουμε τρίγωνο. Αν η ορθή
γωνία ήταν στο Γ θα έχουμε την ισότητα (x-1,y-2,z-1).(x-2,y-1,z-2)=0
ή x2+y2+z2-3(x+y+z)+6=0. τα σημεία που
αληθεύουν την τελευταία ισότητα είναι τα σημεία
της εξωτερικής επιφάνειας της σφαίρας με εξίσωση
(x-3/2)2+(y-3/2)2+(z-3/2)2=3/4. Ένα σημείο
π.χ. είναι το (1,1,2).
=(3,0,0).
Γενικεύοντας παρατηρούμε ότι το Γ βρίσκεται
σ'ένα επίπεδο κάθετο στο διάνυσμα ΑΒ στο σημείο Β.
Η εξίσωσή του είναι 1x-1y+1z=1.2+(-1).1+1.2
ή x-y+z=3. Οιοδήποτε σημείο του επιπέδου αυτού είναι
λύση. Αν η ορθή γωνία ήταν στο Α θα έχουμε επίπεδο
κάθετο στο ΑΒ στο Α και παράλληλο προς το
προηγούμενο με εξίσωση x-y+z=0. Τα σημεία Α,Β,Ο
εξαιρούνται διότι δεν έχουμε τρίγωνο. Αν η ορθή
γωνία ήταν στο Γ θα έχουμε την ισότητα (x-1,y-2,z-1).(x-2,y-1,z-2)=0
ή x2+y2+z2-3(x+y+z)+6=0. τα σημεία που
αληθεύουν την τελευταία ισότητα είναι τα σημεία
της εξωτερικής επιφάνειας της σφαίρας με εξίσωση
(x-3/2)2+(y-3/2)2+(z-3/2)2=3/4. Ένα σημείο
π.χ. είναι το (1,1,2).
2. Να βρεθεί ένα μη-μηδενικό
διάνυσμα, το οποίο είναι κάθετο στα δύο
διανύσματα 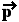 =2
=2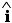 -
-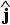 +
+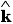 ,
, 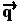 =
=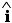 +
+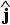 +2
+2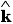 .
.
(Εσωτερικό γινόμενο )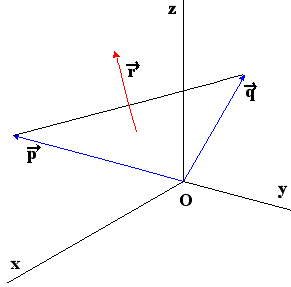
Από αλγεβρικής απόψεως το ζητούμενο διάνυσμα 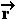 =(x,y,z) θα πρέπει να έχει
εσωτερικό γινόμενο με τα δοθέντα ίσο με το μηδέν.
Δηλαδή να είναι {2x-y+z=0,x+y+2z=0}. Το σύστημα έχει
άπειρες λύσεις που όλες είναι πολλαπλάσια του
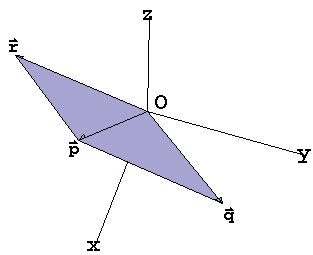
διανύσματος π.χ. (1,1,-1) .Στο σχήμα δίπλα φαίνεται η
γεωμετρική ερμηνεία ότι το ζητούμενο είναι
κάθετο στο επίπεδο που ορίζουν τα δύο δοθέντα
διανύσματα.
=(x,y,z) θα πρέπει να έχει
εσωτερικό γινόμενο με τα δοθέντα ίσο με το μηδέν.
Δηλαδή να είναι {2x-y+z=0,x+y+2z=0}. Το σύστημα έχει
άπειρες λύσεις που όλες είναι πολλαπλάσια του
διανύσματος π.χ. (1,1,-1) .Στο σχήμα δίπλα φαίνεται η
γεωμετρική ερμηνεία ότι το ζητούμενο είναι
κάθετο στο επίπεδο που ορίζουν τα δύο δοθέντα
διανύσματα.
3. Έστω διάνυσμα 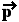 =p 1
=p 1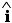 +p2
+p2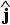 +p 3
+p 3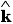 . Εάν οι γωνίες
κατεύθυνσής του είναι π/4,φ,π/4 με τι θα ισούται η
συνιστώσα p2;
. Εάν οι γωνίες
κατεύθυνσής του είναι π/4,φ,π/4 με τι θα ισούται η
συνιστώσα p2;
(Κατευθύνοντα συνημίτονα)
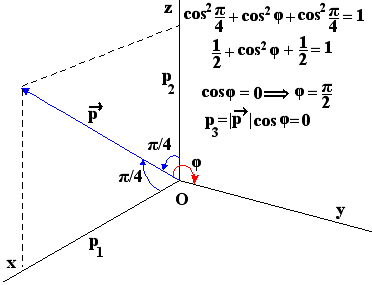
Το 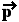 βρίσκεται στο επίπεδο xOz διότι σχηματίζει γωνίες
45ο με τους Οx και Oz ,οπότε η γωνία που
σχηματίζει με τον Oy είναι 90ο, άρα κάθετο
στον άξονα Oy οπότε και η προβολή του στον Οy
είναι μηδέν.
βρίσκεται στο επίπεδο xOz διότι σχηματίζει γωνίες
45ο με τους Οx και Oz ,οπότε η γωνία που
σχηματίζει με τον Oy είναι 90ο, άρα κάθετο
στον άξονα Oy οπότε και η προβολή του στον Οy
είναι μηδέν.
4. Να αποδειχθεί ότι το διάνυσμα 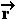 = |
= |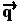 |
|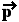 +|
+|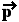 |
|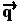 διχοτομεί την γωνία που σχηματίζουν τα
διανύσματα
διχοτομεί την γωνία που σχηματίζουν τα
διανύσματα 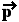 και
και 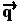 .
.
(Εσωτερικό γινόμενο )
Παρακάτω γίνεται χρήση της σχέσης που δίνεται
και των συνημιτόνων των γωνιών που σχηματίζει το 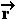 με τα διανύσματα
με τα διανύσματα 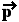 και
και 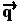 ,καθώς και
της γωνίας που σχηματίζεται μεταξύ των
διανυσμάτων
,καθώς και
της γωνίας που σχηματίζεται μεταξύ των
διανυσμάτων 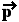 και
και 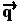 .
.

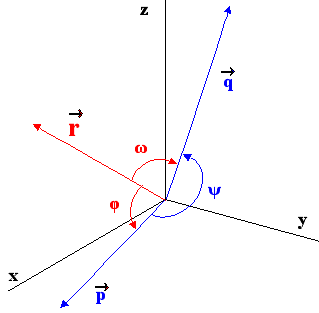
Που δείχνει ότι το 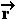 διχοτομεί την γωνία των
διχοτομεί την γωνία των 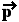 και
και 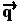 .
.
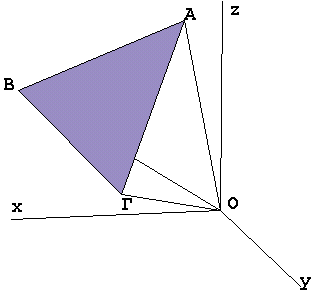
5. Έστω σημεία Α=(a,b,c), B=(c,a,b), Γ=(b,c,a). Να
αποδειχθεί ότι το τρίγωνο ΑΒΓ είναι ισόπλευρο.
(Μέτρο διανύσματος)
Από τα δοθέντα σημεία Α,Β,Γ έχουμε τις σχέσεις:
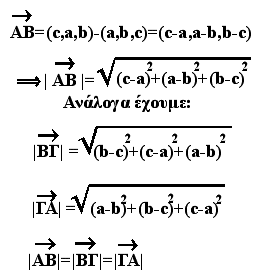
Η τελευταία σχέση δηλώνει ότι το τρίγωνο είναι
ισόπλευρο.
6. Να βρεθούν τα μοναδιαία
διανύσματα που σχηματίζουν γωνία 45ο με το
διάνυσμα 2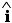 +
+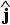 -
-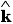 .
.
(Εσωτερικό γινόμενο , Μέτρο διανύσματος)
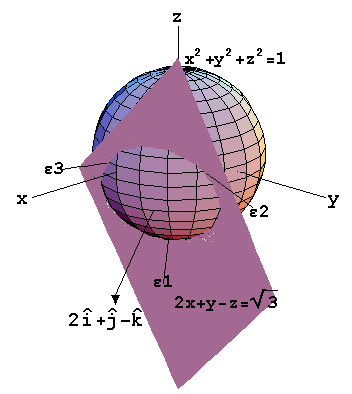 Τα ζητούμενα
διανύσματα θα επαληθεύουν τις σχέσεις:
Τα ζητούμενα
διανύσματα θα επαληθεύουν τις σχέσεις:
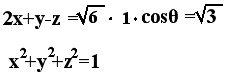
Από τις οποίες φαίνεται ότι τα μοναδιαία
διανύσματα θα είναι, εφ'όσον θεωρήσουμε ότι όλα
τα διανύσματα έχουν ως αρχή τους το Ο, τα
έχοντα το πέρας τους στη κοινή γραμμή της
μοναδιαίας σφαίρας με κέντρο το Ο και ακτίνα 1 και
το επίπεδο 2x+y-z=3(1/2). Στο σχήμα οι ευθείες
ε1,ε2,ε3, είναι τρείς φορείς 3 τυχαίων διανυσμάτων
που είναι μοναδιαία και σχηματίζουν γωνία 45ο
με το δοθέν διάνυσμα και έχουν αρχή το Ο και πέρας
την περιφέρεια κύκλου που είναι η τομή του
επιπέδου και της σφαίρας.
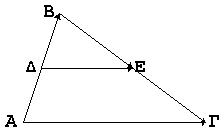
7. Χρησιμοποιώντας διανύσματα να
δειχθεί ότι το ευθύγραμμο τμήμα που συνδέει τα
ενδιάμεσα σημεία δύο πλευρών ενός τριγώνου είναι
παράλληλο προς την τρίτη πλευρά και έχει το μισό
της μήκος.
(Πρόσθεση , Παράλληλα)

8. Να διαπιστωθεί ότι τα διανύσματα 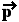 =(1,-1,0),
=(1,-1,0), 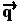 =(2,2,1) είναι μη
συγγραμμικά και ότι το
=(2,2,1) είναι μη
συγγραμμικά και ότι το 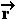 =(-1,-3,-1) είναι συνεπίπεδο με αυτά. Επίσης να
εκφρασθεί το
=(-1,-3,-1) είναι συνεπίπεδο με αυτά. Επίσης να
εκφρασθεί το 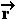 ως
γραμμικός συνδυασμός των
ως
γραμμικός συνδυασμός των 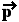 ,
, 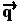 δηλαδή στη μορφή
δηλαδή στη μορφή 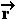 =λ
=λ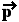 + μ
+ μ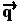 όπου λ,μ αριθμοί.
όπου λ,μ αριθμοί.
(Παράλληλα , Συνεπίπεδα)
Τα διανύσματα όχι συγγραμμικά διότι το ένα δεν
μπορεί να γραφτεί σαν πολλαπλάσιο του άλλου. Ως
μη-συγγραμμικά και με κοινή αρχή το Ο ορίζουν ένα
επίπεδο. Τώρα το 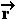 =(-1,-3,-1)
για να βρίσκεται στο ίδιο επίπεδο με τα
=(-1,-3,-1)
για να βρίσκεται στο ίδιο επίπεδο με τα 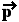 =(1,-1,0),
=(1,-1,0), 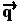 =(2,2,1) θα
πρέπει να είναι γραμμικός συνδυασμός τους. Η
σχέση
=(2,2,1) θα
πρέπει να είναι γραμμικός συνδυασμός τους. Η
σχέση 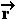 =λ
=λ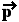 + μ
+ μ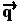 δίνει το
σύστημα {-1=λ+2μ,-3=-λ+2μ,-1=μ}. Έχει λύση το σύστημα και
είναι {λ=1,μ=-1}. Άρα και τα τρία βρίσκονται στο ίδιο
επίπεδο. Είναι δε
δίνει το
σύστημα {-1=λ+2μ,-3=-λ+2μ,-1=μ}. Έχει λύση το σύστημα και
είναι {λ=1,μ=-1}. Άρα και τα τρία βρίσκονται στο ίδιο
επίπεδο. Είναι δε 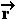 =1.
=1.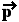 + (-1).
+ (-1).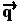 . Ισοδυνάμως
η ορίζουσα των συντεταγμένων των τριών
διανυσμάτων πρέπει να είναι μηδέν.Πράγματι
. Ισοδυνάμως
η ορίζουσα των συντεταγμένων των τριών
διανυσμάτων πρέπει να είναι μηδέν.Πράγματι
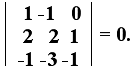






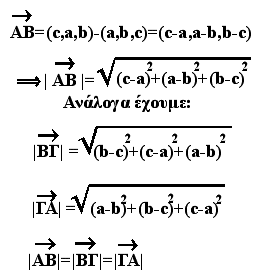
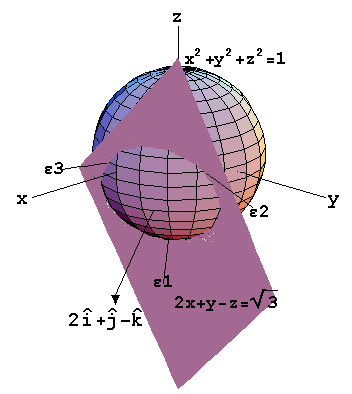 Τα ζητούμενα
διανύσματα θα επαληθεύουν τις σχέσεις:
Τα ζητούμενα
διανύσματα θα επαληθεύουν τις σχέσεις: