Μία από τις πιό σημαντικές δομές που χρησιμοποιούνται στη λογική και στην επιστήμη των υπολογιστών είναι τα δένδρα. Ένα δένδρο είναι κάτι που μοιάζει όπως το παρακάτω :
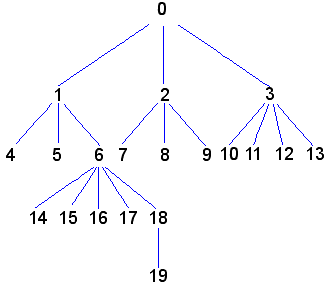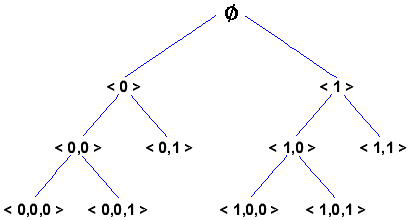
Έχει κόμβους διατεταγμένους μερικά. Στη κορυφή υπάρχει ο κόμβος (κενό σύνολο) και ονομάζεται η ρίζα του δένδρου. Ένας κόμβος σε ένα δένδρο μπορεί να έχει έναν ή περισσότερους άμεσα επόμενους κόμβους. Άν ένας κόμβος έχει περισσότερους από έναν επόμενους, τότε λέμε ότι το δένδρο διακλαδίζεται σε αυτόν τον κόμβο.

Ορισμός :
i) Μία μερική διάταξη είναι ένα σύνολο S με μία διμελή σχέση σε αυτό που συνήθως τη λέμε " μικρότερο από " και συμβολίζεται με , η οποία είναι μεταβατική και αντιανακλαστική :

x y   και   y z        x z    και

το x δεν είναι μικρότερο από το x για κάθε x

ii) Η μερική διάταξη είναι μία γραμμική διάταξη, αν επίσης ικανοποιεί τον νόμο της τριχοτομίας :

x y   ή   x = y   ή   y x

iii) Μία γραμμική διάταξη είναι καλή διάταξη, αν δεν υπάρχει σύνολο στοιχείων x₀ , x₁ , x₂ , . . .   του S τέτοιο που    . . . x₂ x₁ x₀. Δηλαδή αν δεν υπάρχει άπειρη φθίνουσα αλυσίδα .

iv)

x y      x y   ή   x = y

x y      y x

Ορισμός :
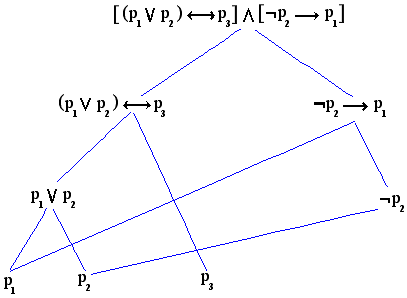
Ένα δένδρο είναι ένα σύνολο Τ (του οποίου τα στοιχεία καλούνται κόμβοι) μερικά διατεταγμένο από την   _Τ , με μοναδικό ελάχιστο σημείο που λέγεται ρίζα , στο οποίο οι κόμβοι, που προηγούνται κάθε κόμβου, είναι καλά διατεταγμένοι από την   _Τ .
Ένα μονοπάτι σ'ένα δένδρο Τ είναι ένα μέγιστο γραμμικά διατεταγμένο υποσύνολο του Τ.

Άσκηση :
Δώστε ένα παράδειγμα ενός πεπερασμένα διακλαδιζόμενου δένδρου.
Απάντηση :

2. Προτασιακή Λογική

Οι προτάσεις είναι δηλώσεις και η προτασιακή λογική περιγράφει και μελετά τους τρόπους με τους οποίους οι δηλώσεις συνδυάζονται για να σχηματίσουν άλλες δηλώσεις. Για να τυποποιήσουμε τη λογική των προτάσεων αρκεί να εισάγουμε σύμβολα για τις απλές προτάσεις μαζί με κάποιους συνδέσμους και μερικά βοηθητικά σύμβολα. Από τις απλές προτάσεις μέσω των συνδέσμων κατασκευάζονται σύνθετες προτάσεις.

Ορισμός :
Η γλώσσα Γ του προτασιακού λογισμού αποτελείται από :

i)  προτασιακές μεταβλητές : p0 , p1 , p2 , . . .

ii)  συνδέσμους : , , , ,

iii)  παρενθέσεις : ( , )

Το όνομα και η σημασία των συνδέσμων είναι :

: λέγεται σύζευξη και σημαίνει " και "

: λέγεται διάζευξη και σημαίνει " ή "

: λέγεται άρνηση και σημαίνει " όχι "

: λέγεται συνεπαγωγή και σημαίνει " αν . . . τότε . . . "

: λέγεται ισοδυναμία και σημαίνει " αν και μόνον αν "

Μ( Γ ) = { p₀ , p₁ , p₂ , . . . } το σύνολο των προτασιακών μεταβλητών της Γ.
Κάθε πεπερασμένη ακολουθία συμβόλων της Γ λέγεται έκφραση.
Για παράδειγμα ( p₀ ) , p₁ p₂ , p₀p₁p₃ είναι εκφράσεις της Γ.
Το σύνολο των εκφράσεων της Γ συμβολίζεται με Ε( Γ ). Όλες όμως οι εκφράσεις δεν μπορούν να θεωρηθούν προτάσεις όπως φαίνεται από τα παραδείγματα. Οι προτάσεις της Γ είναι ένα υποσύνολο του Ε( Γ ) , που κατασκευάζεται με ορισμένους κανόνες σχηματισμού. Το σύνολο των προτάσεων ( προτασιακών τύπων ) της Γ συμβολίζεται με Τ( Γ ) και ορίζεται όπως παρακάτω :

Ορισμός :
 i) Κάθε προτασιακή μεταβλητή είναι προτασιακός τύπος ( M( Γ ) T( Γ ) ) .
ii) Αν οι   ,   είναι προτασιακοί τύποι , τότε και οι εκφράσεις , , , είναι προτασιακοί τύποι .
Ο παραπάνω ορισμός δίνει έναν αλγόριθμο με τον οποίο μπορούμε να αποφασίσουμε σε πεπερασμένο αριθμό βημάτων αν μία έκφραση είναι ή όχι πρόταση (προτασιακός τύπος).
Η διαδικασία του ελέγχου γίνεται με τη βοήθεια δενδροδιαγραμμάτων ( δένδρων ).
Για παράδειγμα στην πρόταση [ ( p₁p₂ ) p₃ ](p₃p₁) αντιστοιχεί το παρακάτω δένδρο ανάλυσης της πρότασης , που δείχνει επίσης πως η πρόταση κατασκευάζεται από προτασιακές μεταβλητές .

Σε κάθε πρόταση αντιστοιχεί ένα δένδρο ανάλυσης .

Ασκήσεις
1) Αποφασίστε αν η έκφραση   ( p₁p₂ ) p₂p₃   είναι πρόταση ή όχι .
Aπάντηση
Προσπαθούμε να γράψουμε το δένδρο ανάλυσης της έκφρασης , ακολουθώντας τους κανόνες σχηματισμού προτάσεων που μας επιτρέπει ο ορισμός .



Βλέπουμε ότι τα κλαδιά του δένδρου δεν απολήγουν όλα σε προτασιακές μεταβλητές. Άρα η παραπάνω έκφραση δεν είναι πρόταση.


2) Είναι η έκφραση   [ ( p₁p₂) p₃ ][p₂p₁ ]   πρόταση ;
Aπάντηση


Επομένως είναι πρόταση.

3) Δείξτε ότι η έκφραση   ( p₁( p₁ ( p₂p₃ ) )) ( p₃ p₄ )   είναι πρόταση.
Απάντηση


4) Είναι η έκφραση   p₁ ( p₁ ( p₁ ( p₁ p₁ ) ) )   πρόταση ;
Απάντηση

Ευρετήριο

Επόμενο