Δύο απλά γραφήματα G₁ και G₂ ονομάζονται ισομορφικά, εάν υπάρχει συνάρτηση  f : V(G₁ ) V(G₂ ) , για την οποία ισχύει ότι οι κορυφές κορυφές u , υ είναι γειτονικές στο G₁ , εάν και μόνο εάν, οι κορυφές  f( u ), f( υ ) είναι γειτονικές στο G₂. Η συνάρτηση   f ονομάζεται ισομορφισμός από το G₁ στο G₂ .
Τα γραφήματα του σχήματος 1.3 είναι δύο ισομορφικά γραφήματα.
Πράγματι υπάρχει η συνάρτηση  f : V(G₁ ) V(G₂ ) με  f( u₁ ) = u₂ ,  f( υ₁ ) = υ₂ ,  f( x₁ ) = x₂ ,  f( w₁ ) = w₂ , η οποία έχει την παραπάνω ιδιότητα.

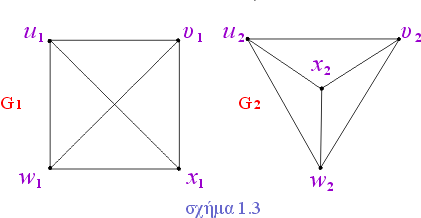
1.3 Υπογραφήματα

Ένα γράφημα Η είναι υπογράφημα κάποιου γραφήματος G (αυτό συμβολίζεται με H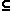G ), εάν

(i) V(H)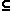V(G) ,

(ii) E(H)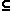E(G) και

(iii) η ψH είναι περιορισμός της ψG στο E(H).

Έστω ότι V' είναι ένα μη κενό υποσύνολο του V(G). Το υπογράφημα του G, που έχει σαν σύνολο κορυφών του το V' και σαν σύνολο ακμών του τις ακμές εκείνες του G που έχουν και τα δύο άκρα τους στο V' και συμβολίζεται με G[V']
Έστω Ε' μη κενό υποσύνολο του E(G). Το υπογράφημα του G, που έχει σαν σύνολο ακμών του το Ε' και σαν σύνολο κορυφών του τα άκρα των ακμών που ανήκουν στο Ε', λέμε ότι προέρχεται από το Ε' και συμβολίζεται με G[Ε'].
Έστω V'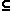V(G). Με G - V' συμβολίζουμε το γράφημα που προκύπτει από το G εάν διαγράψουμε τις κορυφές εκείνες που ανήκουν στο V' καθώς επίσης και τις ακμές των οποίων τουλάχιστον ένα άκρο ανήκει στο V'.
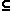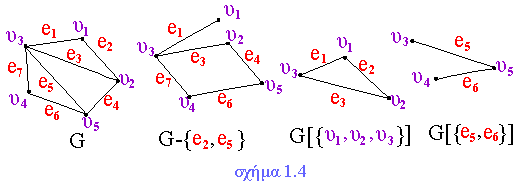
Έστω E'E(G). Με G - E' συμβολίζουμε το γράφημα που προκύπτει από το G, εάν διαγράψουμε τις ακμές που αποτελούν στοιχεία του E'. (Βλέπε σχήμα 1.4 για παραδείγματα των πιο πάνω ορισμών).

Προηγούμενο

Ευρετήριο

Επόμενο