Ένα γράφημα G είναι μια διατεταγμένη τριάδα (V(G) , E(G) , ψ_G), η οποία αποτελείται :

(i)	από ένα σύνολο V(G) , όπου V(G) , τα στοιχεία του οποίου ονομάζονται κορυφές
(ii)	ένα σύνολο Ε(G), όπου Ε(G)V(G) τα στοιχεία του οποίου ονομάζονται ακμές και
(iii)	από μια συνάρτηση ψG , βάσει της οποίας σε κάθε ακμή του G αντιστοιχεί ένα μη διατεταγμένο ζεύγος (όχι απαραίτητα διαφορετικών) κορυφών του G.

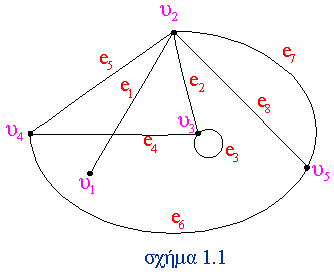
Παράδειγμα 1.1 :
G=(V(G) , E(G) , ψ_G) όπου V(G)={ υ₁ , υ₂ , υ₃ , υ₄ , υ₅ } , E(G)={ e₁ , e₂ , e₃ , e₄ , e₅ , e₆ , e₇ , e₈ } , και όπου η ψ_G ορίζεται ως εξής:

ψG ( e1 ) = { υ1 , υ2 } , ψG ( e2 ) = { υ2 , υ3 } , ψG ( e3 ) = { υ3 , υ3 } , ψG ( e4 ) = { υ3 , υ4 } ,

ψG ( e5 ) = { υ2 , υ4 } , ψG ( e6 ) = { υ4 , υ5 } , ψG ( e7 ) = { υ2 , υ5 } , ψG ( e8 ) = { υ2 , υ5 }

Η μέχρι τώρα ορολογία που χρησιμοποιήσαμε ( ακμές , κορυφές , κ.λ.π.) προέρχεται από την εξής γραφική παράσταση των γραφημάτων:
Κάθε κορυφή απεικονίζεται μ' ένα σημείο στο επίπεδο και κάθε ακμή με μια γραμμή που συνδέει το ζεύγος των κορυφών στις οποίες αντιστοιχεί, δηλαδή η ακμή e συνδέει τις κορυφές u και υ αν και μόνο αν ψ(G) = { u , υ }.
Στο σχήμα 1.1 έχουμε την γραφική παράσταση του γραφήματος G του παραδείγματος 1.1 Εδώ θα πρέπει να παρατηρήσουμε, ότι η γραφική παράσταση ενός γραφήματος G εκφράζει απλώς την σχέση που υπάρχει μεταξύ των κορυφών του και των ακμών του, έτσι όπως καθορίζεται αυτή από την συνάρτηση ψ_G . Επομένως οι θέσεις των σημείων και γραμμών στο επίπεδο δεν έχουν σημασία.
Για παράδειγμα, στο σχήμα 1.2 έχουμε ένα διαφορετικό τρόπο γραφικής παράστασης του γραφήματος G του παραδείγματος. 1.1.
Ο ορισμός του γραφήματος δεν αποκλείει δύο διαφορετικές ακμές ενός γραφήματος G να αντιστοιχούν στο ίδιο ζεύγος κορυφών , δηλαδή μπορεί να υπάρχουν e₁ , e₂ E(G) με e₁ e₂ , έτσι ώστε ψ_G ( e₁ ) = ψ_G ( e₂ ) = { u , υ }.
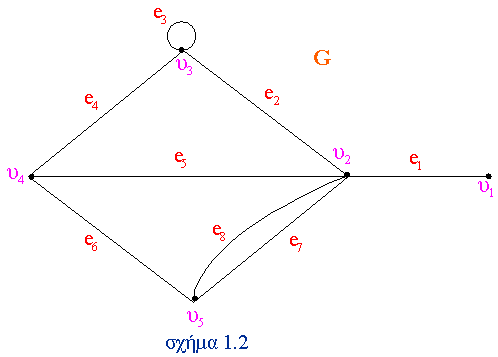
Σε μια τέτοια περίπτωση οι ακμές αυτές ονομάζονται παράλληλες ή πολλαπλές.
Επίσης, δεν αποκλείεται μια ακμή του G να αντιστοιχεί σε ζεύγος κορυφών της μορφής { υ , υ } , δηλαδή μπορεί να υπάρχει e E(G) , έτσι ώστε ψ_G ( e ) = { υ , υ }. Μια τέτοια ακμή ονομάζεται βρόχος.
Στο γράφημα του σχήματος 1.2 οι ακμές e₇ , e₈ είναι πολλαπλές ακμές, ενώ η ακμή e₃ είναι βρόχος.
Εάν ένα γράφημα δεν περιέχει πολλαπλές ακμές και βρόχους, τότε ονομάζεται απλό γράφημα.
Ένα γράφημα G ονομάζεται πεπερασμένο, εάν τα σύνολα V(G) και E(G) είναι πεπερασμένα. Εμείς θα ασχοληθούμε μόνο με πεπερασμένα γραφήματα.
Επομένως, όταν λέμε γράφημα ουσιαστικά εννοούμε πεπερασμένο γράφημα.
Εάν e E(G) , u , υ V(G) και ψ_G ( e ) = { u , υ } τότε χρησιμοποιείται η πιο κάτω ορολογία.

α) Η ακμή e συνδέει τις κορυφές u και υ.

β) Οι κορυφές u και υ αποτελούν τα άκρα της ακμής e.

γ) Οι κορυφές u και υ είναι γειτονικές.

δ) Η κορυφή u είναι προσκείμενη στην κορυφή υ και αντίστροφα.

Όλες οι παραπάνω προτάσεις είναι ισοδύναμες.
Ο αριθμός των κορυφών και ακμών ενός γραφήματος G συμβολίζεται με v(G) και ε(G) αντίστοιχα ή πιο απλά με v και ε .

Ευρετήριο

Επόμενο