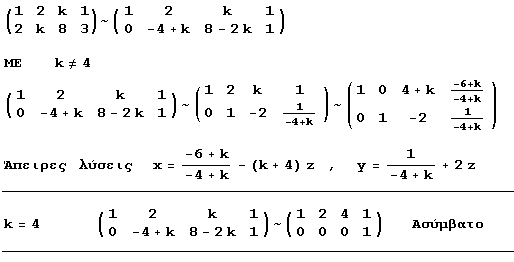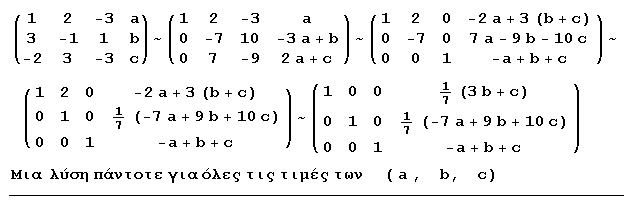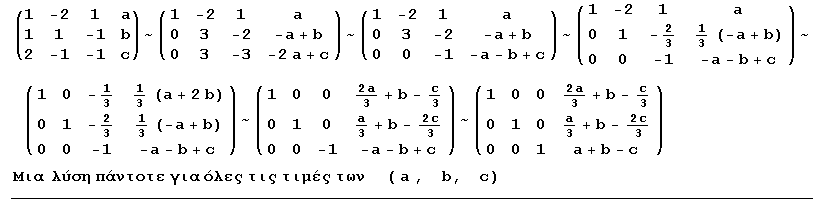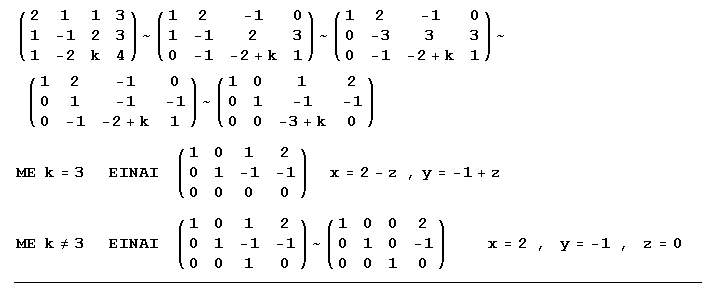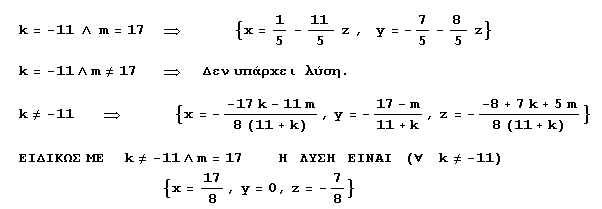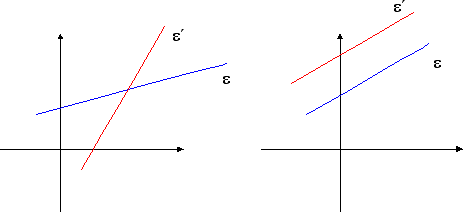
Άπειρες λύσεις
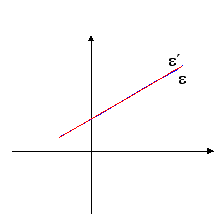
| a1x+b1y=c1 a2x+b2y=c2 |
| kx+y+z = 1 | x-3z = -3 | x+2y+kz = 1 | x + z = 4 |
| x+ky+z = 1 | 2x+ky-z = -2 | 2x+ky+8z = 3 | 2x-y+z = 0 |
| x+y+kz = 1 | x+2y+kz = 1 | 3x+ky = 1 |
| α) | x+2y-3z = a 3x-y+z = b -2x+3y-3z = c | β) | x-2y+z = a x+y-z = b 2x-y-z = c |
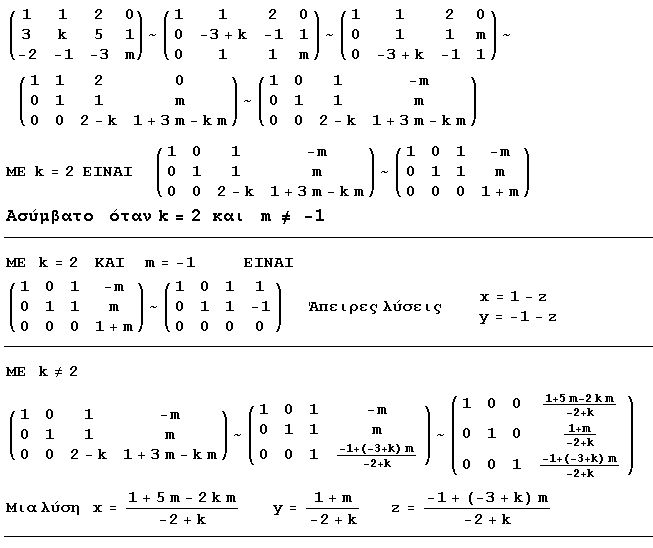
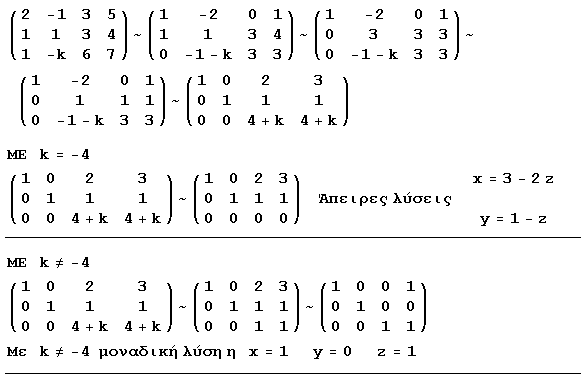
| a) | x+y+2z = 0 3x+ky+5z = 1 -2x-y-3z = m | b) | 2x+y+z = 3 x-y+2z = 3 x-2y+kz = 4 | c) | 2x-y+3z = 5 x+y+3z = 4 x-ky+6z = 7 |
| 3x - y + 5z = 2 |
| x - 2y - z = 3 |
| 8x + k y = m |