1.6.2 Διμερή γραφήματα
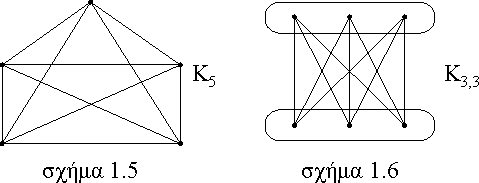
Ένα γράφημα G ονομάζεται διμερές, εάν το σύνολο των κορυφών του μπορεί να χωριστεί σε δύο σύνολα X και Y, ξένα μεταξύ τους, έτσι ώστε κάθε ακμή του G να συνδέει ένα στοιχείο του X με ένα στοιχείο του Y. Το ζεύγος ( X ,Y ) ονομάζεται διαμερισμός του G.Εάν τώρα σ' ένα διμερές γράφημα G με διαμερισμό ( X ,Y ), όπου |X | = m και |Y | = n, κάθε κορυφή του Χ είναι γειτονική με όλες τις κορυφές του Y, τότε λέμε ότι το G είναι πλήρες διμερές γράφημα και συμβολίζεται με Km,n (βλέπε σχ. 1.6)
1.6.3. Κανονικά γραφήματα
Ένα γράφημα G ονομάζεται k - κανονικό εάν dG(x)=k
Χρησιμοποιώντας το θεώρημα 1.1 μπορούμε εύκολα να αποδείξουμε το παρακάτω πόρισμα.
Πόρισμα 1.2: Εάν το G είναι k - κανονικό γράφημα, όπου το k είναι περιττός αριθμός, τότε το G περιέχει άρτιο αριθμό κορυφών.
1.7 Πίνακες γειτνίασης και πρόσπτωσης
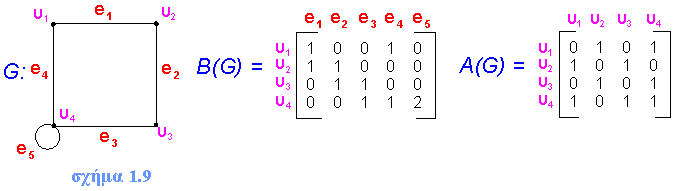
Σ' ένα γράφημα G αντιστοιχεί ένας πίνακας ν x ε, ο οποίος ονομάζεται πίνακας πρόσπτωσης. Εάν οι κορυφές του G είναι οι υ1 , υ2 , . . . , υνκαι οι ακμές του οι e1 , e2 , . . . , eε , τότε ο πίνακας πρόσπτωσης του G είναι ο πίνακας B( G ) = [ bij ] , όπου bij συμβολίζει πόσες φορές η κορυφή υi, είναι άκρο της ακμής ej (δηλαδή το bij μπορεί να πάρει τις τιμές 0,1,2 ,την τιμή 2 την παίρνει όταν η ακμή ej είναι βρόχος και έχει για άκρα της την υi ).
Ένας άλλος πίνακας, ο οποίος αντιστοιχεί σ' ένα γράφημα G, είναι ο πίνακας γειτνίασης. Αυτός είναι ο ν x ν πίνακας Α( G ) = [ aij ] όπου aij είναι ο είναι ο αριθμός των ακμών που συνδέουν τις κορυφές υi και υj .
Παράδειγμα 1.2:
Προηγούμενο |
Ευρετήριο | Επόμενο |