ΣΥΝΔΥΑΣΤΙΚΗ

1.  Πόσοι ακέραιοι υπάρχουν μεταξύ του 100 και του 199, οι οποίοι έχουν διαφορετικά ψηφία;

Απάντηση: 72

2. Πόσοι από τους ακέραιους της προηγούμενης άσκησης είναι περιττοί;

3. Πόσοι από τους πρώτους 10000 θετικούς ακέραιους έχουν διαφορετικά ψηφία;

4. Πόσους περιττούς ακέραιους μπορούμε να σχηματίσουμε με τα ψηφία 1, 2, 3, 4, 5 οι οποίοι έχουν 4 ψηφία και τα ψηφία αυτά είναι διαφορετικά μεταξύ τους;

5. Πόσοι πενταψήφιοι ακέραιοι υπάρχουν οι οποίοι είναι μεγαλύτεροι του 53000 και έχουν ταυτόχρονα τις εξής ιδιότητες: i) τα ψηφία τους είναι διαφορετικά και ii) δεν εμφανίζονται σε αυτούς τα ψηφία 0 και 9;

Απάντηση: 3120

6. Εστω το σύνολο Α = { 0, 1 }. Λέξεις 0 - 1 ονομάζουμε τις λέξεις που έχουν για γράμματα τους στοιχεία του Α. α) Πόσες λέξεις 0 - 1 υπάρχουν οι οποίες έχουν οκτώ γράμματα και αρχίζουν με 1100; β) Πόσες 0 - 1 λέξεις υπάρχουν οι οποίες έχουν οκτώ γράμματα εκ των οποίων δύο ακριβώς είναι 1;

Απάντηση: 16--28

7. Τα γράμματα Α, Β, Γ, Δ χρησιμοποιούνται για να σχηματίσουμε λέξεις μήκους 3. α) Πόσες λέξεις υπάρχουν που περιέχουν το γράμμα Α, επιτρεπομένων των επαναλήψεων; β) Πόσες λέξεις υπάρχουν που αρχίζουν με Α επιτρεπομένων των επαναλήψεων;

Απάντηση: 37--16

8. Ενα διαγώνισμα πολλαπλής επιλογής περιέχει ν ερωτήσεις με μ_1, μ₂, μ₃, ... , μ_ν απαντήσεις αντιστοίχως. Ο εξεταζόμενος σημειώνει μια απάντηση σε κάθε ερώτηση. Να υπολογισθεί το πλήθος των τρόπων που μπορεί να απαντηθεί το διαγώνισμα.

9. Το Αγγλικό αλφάβητο περιέχει 26 γράμματα εκ των οποίων τα 5 είναι φωνήεντα. Πόσες λέξεις μήκους  5 μπορούμε να σχηματίσουμε χρησιμοποιώντας 3 διαφορετικά σύμφωνα και 2 διαφορετικά φωνήεντα;

Απάντηση: 1596000

10.  Πόσες από τις λέξεις της άσκησης 9 περιέχουν το γράμμα b;

Απάντηση: 228000

11. Πόσες από τις λέξεις της άσκησης 9 αρχίζουν με a και περιέχουν το b;

Απάντηση: 18240

12. Πόσες από τις λέξεις της άσκησης 9 αρχίζουν με b και τελειώνουν με c;

Απάντηση:1140

13. Ενας καθηγητής συγκεντρώνει ν εργασίες από ισάριθμους φοιτητές και σκοπεύει να τις δώσει στους φοιτητές για να τις διορθώσουν. Η επιστροφή των εργασιών πρέπει να γίνει με ένα τέτοιο τρόπο, έτσι ώστε να αποκλεισθεί η περίπτωση, κάποιος φοιτητής να διορθώσει τη δική του εργασία. Με πόσους τρόπους μπορεί να γίνει η κατανομή των εργασιών;

Απάντηση:    ν! /e

14. Βρείτε το πλήθος α) των διψήφιων αρτίων αριθμών β) διψήφιων περιττών αριθμών γ) διψήφιων περιττών αριθμών με διαφορετικά ψηφία και δ) διψήφιων αρτίων αριθμών με διαφορετικά ψηφία.

Απάντηση:45---45---40----41

15. Παλινδρομική λέγεται μια πεπερασμένη ακολουθία χαρακτήρων, που διαβάζεται το ίδιο από τον πρώτο χαρακτήρα προς τον τελευταίο και αντιστρόφως. Βρείτε το πλήθος των επταψήφιων και οκταψήφιων τέτοιων ακολουθιών, στις οποίες κάθε ψηφίο δεν μπορεί να εμφανίζεται περισσότερες από δύο φορές, με τον τρόπο που περιγράφηκε παραπάνω.

Απάντηση:4536

16. Δείξτε ότι ένας παλινδρομικός αριθμός στο δεκαδικό σύστημα μήκους 2κ διαιρείται με το 11.

17. Βρείτε το πλήθος των διαιρετών (εκτός της μονάδας και του εαυτού του) του αριθμού 441000.

Απάντηση:142

18. Αν ένα σύνολο Χ έχει ν στοιχεία, πόσα στοιχεία έχει το δυναμοσύνολο του Ρ(Χ);

Απάντηση: 

19. α) Βρείτε το πλήθος των θετικών ακεραίων με ν ψηφία, στους οποίους δύο διαδοχικά ψηφία δεν είναι ίδια. β) Βρείτε το πλήθος των αρτίων τέτοιων αριθμών.

Απάντηση:   

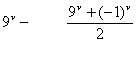
20. Με πόσους τρόπους ν άνδρες και ν γυναίκες μπορούν να καθήσουν σε μια γραμμή με 2ν καρέκλες, ώστε τα δύο φύλα να εναλλάσσονται;

Απάντηση:

21. Κυκλική μετάθεση είναι μια διάταξη ν διακεκριμένων αντικειμένων γύρω από ένα κύκλο (ή γύρω από μια κλειστή γραμμή). Βρείτε το πλήθος των κυκλικών μεταθέσεων ν ξεχωριστών αντικειμένων.

Απάντηση: (ν-1)!

22. Στο Lotto ένα δελτίο συμπληρώνεται με την επιλογή 6 από 49 αριθμούς. Ποιό είναι το πλήθος των δελτίων που μπορούν να συμπληρωθούν για να έχουμε σίγουρο εξάρι; Αν έχουν κληρωθεί 6 αριθμοί πόσα είναι τα διαφορετικά δελτία που κερδίζουν 5-άρι και πόσα τα διαφορετικά δελτία που κερδίζουν 4-άρι;

Απάντηση:13983816-----258 ----- 13545

23. Αποδείξτε τη σχέση: C(ν,μ).C(μ,κ) = C(ν,κ).C(ν-κ,μ-κ), όπου κ>= μ>= ν φυσικοί.

24. Ενας σύλλογος έχει ν μέλη. Το Διοικητικό Συμβούλιο του συλλόγου έχει μ μέλη και η Εκτελεστική Επιτροπή του συλλόγου αποτελείται από κ μέλη του Διοικητικού Συμβουλίου. Πόσοι τρόποι επιλογής υπάρχουν για τα κ μέλη της Εκτελεστικής Επιτροπής από τα ν μέλη του συλλόγου; Εργαζόμενοι με δύο τρόπους αποδείξτε τη σχέση της άσκησης 23.

25. Δείξτε ότι αν ν είναι πρώτος αριθμός C(ν,μ) διαιρείται με το ν, για μ=1,2,...,ν-1.

26. Βρείτε το πλήθος των πενταψήφιων θετικών ακεραίων, τέτοιων ώστε κάθε ψηφίο να είναι μικρότερο του προηγουμένου ψηφίου.

Απάντηση:252

27. Μια υπάλληλος έχει 11 συναδέλφους εκ των οποίων 8 είναι άνδρες. Θέλει να καλέσει σε δείπνο μερικούς συναδέλφους της. Πόσους τρόπους επιλογής έχει α) αν θέλει να καλέσει τουλάχιστον 9 β) αν καλέσει όλες τις γυναίκες και τόσους άνδρες, ώστε ο αριθμός γυναικών και ανδρών να είναι ίσος.

Απάντηση:67 ---- 70

28.  Σε ένα δημοτικό συμβούλιο μετέχουν 10 μέλη από την παράταξη Α και 11 μέλη από την παράταξη Β. Από την παράταξη Α 4 μέλη είναι γυναίκες και από την παράταξη Β 3 μέλη είναι γυναίκες. Βρείτε το πλήθος των τρόπων σχηματισμού μιας οκταμελούς επιτροπής, στην οποία μετέχουν ίσος αριθμός ανδρών και γυναικών και ίσος αριθμός μελών από τις δύο παρατάξεις.

Απάντηση: 18382

29. Σε μια επιτροπή μετέχουν 12 μέλη, που κάθονται γύρω από ένα τραπέζι. Υπάρχει μια θέση ειδικά για τον πρόεδρο. Τρία μέλη της επιτροπής και ο πρόεδρος αποτελούν μια υποεπιτροπή. Βρείτε το πλήθος των τρόπων που μπορούν να καθήσουν τα μέλη της επιτροπής αν α) τα μέλη της υποεπιτροπής κάθονται μαζί σαν block και β) τα μέλη της υποεπιτροπής ανά 2 δεν μπορούν να κάθονται δίπλα.

Απάντηση:2177280-----20321280

30. Σε μια σχολή, υπάρχουν 12 φοιτητές που παίρνουν το μάθημα των Μαθηματικών (Α), 20 που παίρνουν το μάθημα της Βιολογίας (Β), 20 που παίρνουν το μάθημα της Χημείας (Γ) και 8 που παίρνουν το μάθημα της Φυσικής (Δ). Επίσης υπάρχουν 5 φοιτητές που παίρνουν τα μαθήματα Α και Β, 7 που παίρνουν τα Α και Γ, 4 παίρνουν Α και Δ, 16 παίρνουν Β και Γ, 4 παίρνουν Β και Δ, 3 παίρνουν Γ και Δ. Ακόμη 3 φοιτητές παίρνουν τα μαθήματα Α, Β, Γ, 2 φοιτητές παίρνουν τα Α, Β, Δ, 2 παίρνουν τα Β, Γ, Δ και 3 φοιτητές παίρνουν τα Α, Γ, Δ. Τέλος 2 φοιτητές παίρνουν όλα τα μαθήματα. Βρείτε το πλήθος των φοιτητών της σχολής, αν είναι γνωστό ότι 71 φοιτητές δεν έχουν δηλώσει ακόμη μαθήματα.

Απάντηση:100

31. Βρείτε το πλήθος των θετικών ακεραίων που είναι μικρότεροι του 601 και ΔΕΝ διαιρούνται με το 3, το 5 και το 7.

Απάντηση: 275

32. Υπάρχουν 4 δρόμοι μεταξύ των πόλεων Α και Β και 6 δρόμοι μεταξύ των πόλεων Β και Γ. Βρείτε το πλήθος όλων των τρόπων μετάβασης Α) από την πόλη Α στην πόλη Γ β) από την Α και Γ και πίσω στην πόλη Α και γ) από την πόλη Α στη Γ και πάλι πίσω στη Α χωρίς να χρησιμοποιηθεί δύο φορές ο ίδιος δρόμος.

Απάντηση:24 ---576---360

33. Βρείτε το πλήθος των τρόπων επιλογής 3 διαφορετικών θετικών ακεραίων από το σύνολο Χ = {1,2,...,100}, έτσι ώστε το άθροισμα τους να διαιρείται με το 3.

Απάντηση:53922

34. Βρείτε το πλήθος των μεταθέσεων των γραμμάτων της λέξης ΧΑΡΑΜΑ.

Απάντηση:120

35. Βρείτε το άθροισμα όλων των τετραψήφιων θετικών ακεραίων που σχηματίζονται από τις μεταθέσεις των αριθμών 1, 2, 3, 4.

Απάντηση:66660

36. Βρείτε το πλήθος των μεταθέσεων των αριθμών {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} στις οποίες α) κανένα από τα blocks 23, 45 και 678 δεν εμφανίζεται και β) κανένα από τα blocks 34, 45 και 738 δεν εμφανίζεται.

Απάντηση: 283080 ----282960

37. Υπάρχουν 8 επιστολές προς 8 διαφορετικούς παραλήπτες. Βρείτε το πλήθος των τρόπων αποστολής των επιστολών, έτσι ώστε μία τουλάχιστον επιστολή να φθάσει στον σωστό παραλήπτη.

Απάντηση: 25487

38. Ενας σύλλογος έχει στο Διοικητικό του Συμβούλιο 8 άνδρες μέλη και 6 γυναίκες μέλη. Από τα μέλη αυτά ένας άνδρας και μια γυναίκα είναι σύζυγοι. Βρείτε το πλήθος των τρόπων σχηματισμού μιας εξαμελούς επιτροπής που θα αποτελείται από 3 άνδρες και 3 γυναίκες, έτσι ώστε στην επιτροπή αυτή να μη μετέχουν και οι δύο σύζυγοι.

Απάντηση: 910

39. Βρείτε το πλήθος των μεταθέσεων των γραμμάτων του ελληνικού αλφαβήτου, οι οποίες δεν περιέχουν τη λέξη ΒΡΑΔΥ.

Απάντηση: 24! -20!

40. Να προσδιοριστεί ο αριθμός των μεταθέσεων των {1, 2, 3, 4, 5, 6} στις οποίες το 3 βρίσκεται μεταξύ των 2 και 4. (Οι 521364, 123456, 145326 είναι παραδείγματα τριών τέτοιων μεταθέσεων).

Απάντηση:240